Théorème de Poncelet-Steiner

La traduction de cet article ou de cette section doit être revue (janvier 2024).

Le contenu est difficilement compréhensible vu les erreurs de traduction, qui sont peut-être dues à l'utilisation d'un logiciel de traduction automatique. Discutez des points à améliorer en page de discussion ou modifiez l'article.

Pour les articles homonymes, voir Théorème de Poncelet, Grand théorème de Poncelet, Poncelet et Steiner.

Dans la branche des mathématiques connue sous le nom de géométrie euclidienne, le théorème de Poncelet-Steiner est l'un des nombreux résultats concernant les constructions à la règle et au compas avec des restrictions supplémentaires imposées aux règles traditionnelles. Ce résultat indique que tout ce qui peut être construit ensemble à la règle et au compas peut être construit à la règle seule, à condition qu'un seul cercle et son centre soient donnés. Ce théorème est lié à l’équivalence du compas rouillé.

Toute construction euclidienne, dans la mesure où les éléments donnés et requis sont des points (ou des lignes), si elle peut être complétée à la fois avec le compas et la règle ensemble, peut être complétée avec la règle seule à condition qu'il existe au moins un cercle avec son centre dans le plan.

Bien qu’un compas puisse faciliter considérablement les constructions, il est sous-entendu qu’elle n’a aucun objectif fonctionnel une fois le premier cercle tracé. Toutes les constructions restent possibles, même s'il est bien entendu que les cercles et leurs arcs ne peuvent être tracés sans le compas. Cela signifie seulement que le compas peut être utilisé à des fins esthétiques plutôt qu’à des fins de construction. Tous les points qui définissent de manière unique une construction, qui peuvent être déterminés à l'aide du compas, sont également déterminables sans, quoique avec plus de difficulté.

Les constructions réalisées conformément à ce théorème — reposant uniquement sur l'utilisation d'une règle sans l'aide d'un compas — sont connues sous le nom de constructions de Steiner. Les constructions de Steiner peuvent impliquer n'importe quel nombre de cercles, y compris aucun, déjà dessinés dans le plan, avec ou sans leurs centres. Ils peuvent également impliquer toutes sortes de formes et de courbes uniques préexistantes dans le plan, à condition que la règle soit le seul outil physique à la disposition du géomètre. Alors que le théorème de Poncelet-Steiner stipule l'existence d'un cercle et de son centre, et affirme qu'un seul cercle équivaut à un compas.

Au X^e siècle, le mathématicien persan Abu al-Wafa' Buzjani (940−998) envisageait des constructions géométriques à l'aide d'une règle et d'un compas à ouverture fixe, dit « compas rouillé ». Les constructions de ce type semblaient avoir une certaine importance pratique puisqu'elles étaient utilisées par les artistes Léonard de Vinci et Albrecht Dürer en Europe à la fin du XV^e siècle. Un nouveau point de vue s'est développé au milieu du XVIe siècle lorsque la taille de l'ouverture était considérée comme fixe mais arbitraire et que la question de savoir combien de constructions d'Euclide pouvaient être obtenues était primordiale^[1].

Le mathématicien de la Renaissance Lodovico Ferrari, élève de Gerolamo Cardano dans un "défi mathématique" contre Niccolò Fontana Tartaglia a pu montrer que "tout Euclide" (c'est-à-dire, les constructions à la règle et au compas dans les six premiers livres des Éléments d'Euclide) pouvaient être réalisées avec une règle et un compas rouillé. En dix ans, des ensembles supplémentaires de solutions ont été obtenus par Cardano, Tartaglia et Benedetti, l'étudiant de Tartaglia. Au cours du siècle suivant, ces solutions furent généralement oubliées jusqu'à ce qu'en 1673, Georg Mohr publie (anonymement et en néerlandais) Euclidis Curiosi contenant ses propres solutions. Mohr avait seulement entendu parler de l'existence des résultats antérieurs et cela l'a amené à travailler sur le problème^[2].

Montrer que "tout Euclide" pouvait être réalisé avec une règle et un compas rouillé n'est pas la même chose que prouver que "toutes" les constructions à la règle et au compas pouvaient être réalisées avec une règle et juste un compas rouillé. Une telle preuve nécessiterait la formalisation de ce qu’une règle et un compas pourraient construire. Ce travail de base a été fourni par Jean-Victor Poncelet en 1822, après avoir été motivé par les travaux de Mohr sur le théorème de Mohr-Mascheroni. Il a également conjecturé et suggéré une preuve possible qu'une règle et un compas rouillé seraient équivalents à une règle et un compas, et de plus, le compas rouillé ne doit être utilisé qu'une seule fois. Le résultat selon lequel "une règle et un cercle unique avec un centre donné équivaut à une règle et un compas" a été prouvé par Jakob Steiner en 1833^[3],[1].

Diverses autres notions, outils, terminologies, etc., sont souvent associées (parfois vaguement) au théorème de Poncelet-Steiner. Certains sont répertoriés ici.

Le terme de « construction de Steiner » fait généralement référence à toute construction géométrique qui utilise uniquement la règle droite, et est parfois simplement appelé « construction uniquement à la règle ». Aucune stipulation n'est faite sur les objets géométriques qui existent déjà dans le plan ou sur leur placement relatif ; de telles conditions sont postulées à l’avance. De plus, aucune implication n’est faite sur ce qui est ou n’est pas possible à construire.

Par conséquent, toutes les constructions adhérant au théorème de Poncelet-Steiner sont des constructions de Steiner, bien que toutes les constructions de Steiner ne respectent pas la condition d'un seul cercle dont le centre est situé dans le plan. Le théorème de Poncelet-Steiner ne nécessite pas de véritable compas — on suppose que le cercle préexiste dans le plan — donc toutes les constructions ici démontrant le théorème de Poncelet-Steiner sont des constructions de Steiner.

Le compas rouillé décrit un compas dont la charnière est tellement rouillée qu'elle est fusionnée de telle sorte que ses pattes - l'aiguille et le crayon - sont incapables d'ajuster la largeur. Essentiellement, il s’agit d’un compas dont la distance est fixe et qui trace des cercles d’un rayon prédéterminé et constant, mais arbitraire. Les cercles peuvent être dessinés centrés en n'importe quel point arbitraire, mais le rayon est immuable.

En tant que construction restreinte de paradigme, les « constructions au compas rouillée » permettent l'utilisation d'une règle et d'un compas à largeur fixe. L’équivalence du compas rouillé s'énonce ainsi :

Tous les points nécessaires pour décrire de manière unique toute construction à la règle et au compas peuvent être obtenus avec une règle et un compas à largeur fixe.

Il est bien entendu entendu que le compas à ouverture arbitraire peut être utilisée à des fins esthétiques ; seul l'arc du compas à largeur fixe peut être utilisé pour la construction.

Dans un certain sens, le compas rouillé est une généralisation et une simplification du théorème de Poncelet-Steiner. Même s’il n’est pas plus puissant, il est certainement plus pratique. Le théorème de Poncelet-Steiner nécessite qu'un seul cercle avec un rayon et un point central arbitraires soit placé dans le plan. Comme c'est le seul cercle dessiné, qu'il ait été dessiné ou non par un compas rouillé est sans importance et équivalent. L'avantage des constructions générales de compas rouillés, cependant, est que le compas peut être utilisé à plusieurs reprises pour redessiner des cercles centrés en n'importe quel point souhaité, bien qu'avec le même rayon, simplifiant ainsi de nombreuses constructions. Naturellement, si toutes les constructions sont possibles avec un seul cercle arbitrairement placé dans le plan, alors on peut sûrement en dire autant d'une règle et d'un compas rouillé, avec lesquels au moins un cercle peut être arbitrairement placé.

On sait qu'une règle et un compas rouillé suffisent pour construire tout ce qui est possible avec une règle et un compas standard - avec la compréhension implicite que des arcs de cercle de rayons arbitraires ne peuvent pas être dessinés et ne doivent être dessinés qu'à des fins esthétiques plutôt que constructives. . Historiquement, cela a été prouvé lorsque le théorème de Poncelet-Steiner a été prouvé, ce qui constitue un résultat plus fort. Le compas rouillé rouillée n’est donc ni plus faible, ni plus fort que le théorème de Poncelet-Steiner.

Le théorème de Poncelet-Steiner réduit l'équivalence du compas rouillé de Ferrari, prétendue à l'époque, à un compas à usage unique :

Tous les points nécessaires pour décrire de manière unique toute construction au compas peuvent être obtenus avec seulement une règle, une fois le premier cercle placé.

Le théorème de Poncelet-Steiner prend le scénario d’un compas rouillé et brise complètement le compas après sa première utilisation.

Ne doit pas être confondu avec le théorème de Huygens-Steiner

Si un seul cercle doit être donné et aucune autre information particulière, le théorème de Steiner implique que le centre du cercle doit être fourni ainsi que l'arc du cercle. Cela se fait en prouvant l'impossibilité de construire le centre du cercle à partir d'une seule règle en utilisant un seul cercle dans le plan, sans son centre. Un argument utilisant les homographies et les coniques de Steiner (en) est utilisé.

Avec un seul cercle prévu dans le plan, son centre ne peut pas être construit par la seule règle.

Un résumé naïf de la preuve est le suivant. Avec l'utilisation d'un outil à règle, seules les transformations projectives linéaires sont possibles, et les transformations projectives linéaires sont des opérations réversibles. Les lignes se projettent sur des lignes sous n'importe quelle transformation projective linéaire, tandis que les coniques se projettent sur des coniques sous une transformation projective linéaire, mais ces dernières sont asymétriques de telle sorte que excentricités, foci, et les centres des cercles ne sont pas conservés. Sous différentes suites de prolongements, le centre ne se projette pas de manière unique et réversible. Ce ne serait pas le cas si des lignes pouvaient être utilisées pour déterminer le centre d’un cercle. Comme les transformations linéaires sont des opérations réversibles et produiraient donc des résultats uniques, le fait que des résultats uniques ne soient pas possibles implique l'impossibilité de constructions de points centraux. Le caractère unique du centre construit dépendrait d'informations supplémentaires qui rendraient la construction réversible.

Il n’est donc pas possible de construire tout ce qui peut être construit avec une règle et un compas avec la seule règle. Par conséquent, les exigences du théorème de Poncelet-Steiner ne peuvent être affaiblies par rapport au centre du cercle. Si le centre du seul cercle donné n'est pas fourni, il ne peut pas être obtenu par une règle seule. De nombreuses constructions sont impossibles avec une règle seule. Il faut quelque chose de plus, et un cercle dont le centre est identifié suffit.

Alternativement, le centre peut être omis avec suffisamment d'informations supplémentaires. Il ne s’agit pas d’une version plus faible du théorème de Poncelet-Steiner, mais simplement d’un cadre alternatif. Ce n'est pas non plus une contradiction avec le théorème de Steiner qui ne postule qu'un seul cercle. L'inclusion de ces informations alternatives suffisantes, qui incluent toujours au moins deux cercles, lève l'ambiguïté des mappages sous les transformations projectives, permettant ainsi à diverses constructions de Steiner de récupérer le centre du cercle.

Chacune de ces alternatives nécessite au moins deux cercles dépourvus de leur centre, ainsi qu'une autre information unique. Certaines alternatives incluent deux cercles concentriques ou concourants, ou trois cercles, ou d'autres variantes dans lesquels les cercles fournis sont dépourvus de leurs centres. Dans chacun, un critère supplémentaire unique mais suffisant est rempli, tel que la concentricité, les points d'intersection, un troisième cercle, etc., respectivement. Dans chacun de ces cas, le centre d'un cercle peut être construit, réduisant ainsi le problème à l'hypothèse du théorème de Poncelet-Steiner (avec l'avantage supplémentaire d'avoir des cercles supplémentaires dans le plan, dont tous les centres peuvent désormais être construits).

Pour prouver le théorème, il faut prouver que chacune des constructions de base du compas et de la règle est possible en utilisant une règle seule (à condition qu'un cercle et son centre existent dans le plan), car ce sont les fondations ou les étapes élémentaires de toutes les autres constructions. C'est-à-dire que toutes les constructions peuvent être écrites comme une série d'étapes impliquant ces cinq constructions de base :

1. Création de la droite passant par deux points existants
2. Créer le cercle passant par un point avec le centre d'un autre point
3. Création du point qui est l'intersection de deux droites existantes non parallèles
4. Créer un ou deux points à l'intersection d'une droite et d'un cercle (s'ils se coupent)
5. Créer un ou deux points à l'intersection de deux cercles (s'ils se croisent).

n^o 1 – Une droite passant par deux points

Cela peut être fait avec une règle seule. Ni un compas ni un cercle ne sont nécessaires.

n^o 2 – Un cercle passant par un point avec un centre défini

Il est entendu que l’arc de cercle ne peut être tracé sans compas. Un cercle est considéré comme étant donné par deux points quelconques, l'un définissant le centre et l'autre existant sur la circonférence au rayon. Une telle paire définit un cercle unique, bien que la réciproque ne soit pas vraie : pour un cercle donné, il n'y a pas de paire unique le définissant. Conformément à l’intention du théorème que nous cherchons à prouver, le cercle réel n’a pas besoin d’être tracé, mais pour des raisons esthétiques.

n^o 3 – Intersection de deux droites

Cette construction peut également être réalisée directement à la règle.

n^o 4, n^o 5 – Intersections impliquant le cercle

Ainsi, pour prouver le théorème, seules les constructions n^o 4 et n^o 5 doivent être prouvées possibles en utilisant uniquement une règle et un cercle donné avec son centre.

Remarques

Tout doute sur les constructions n^o 1 ou n^o 3 s'appliquerait également au paradigme de construction traditionnel impliquant le compas et ne constitue donc pas une préoccupation propre au théorème de Poncelet-Steiner.

La construction n^o 2 ne devrait pas poser de problème. Même s'il est incontestable qu'un cercle unique est défini par un point central et un point sur sa circonférence, la question pertinente est de savoir si cela constitue une information suffisante aux fins de la construction, ou si l'arc dessiné est requis. L'arc de cercle n'est utilisé que dans les paradigmes de construction traditionnels aux fins des intersections cercle-cercle et cercle-droite, dans lesquels l'arc de cercle est utilisé directement pour identifier les points d'intersection. Ainsi, si les constructions n^o 4 et n^o 5 sont satisfiables sans l'arc de cercle avec lequel se croiser, alors cela prouvera la non-nécessité de tracer l'arc. Cela impliquerait donc que la construction n^o 2 est satisfaite par un simple étiquetage de deux points, identifiant le cercle unique.

Dans les constructions générales, il existe souvent plusieurs variantes qui produiront le même résultat. Les choix opérés dans une telle variante peuvent l'être sans perte de généralité. Cependant, lorsqu'une construction est utilisée pour prouver que quelque chose peut être fait, il n'est pas nécessaire de décrire tous ces différents choix et, par souci de clarté de l'exposé, une seule variante sera donnée ci-dessous. Les variantes choisies ci-dessous le sont pour leur omniprésence d'application plutôt que pour leur simplicité dans un ensemble particulier de conditions particulières.

Dans les constructions ci-dessous, un cercle défini par un point central P et un point sur sa circonférence, Q, par lequel passe l'arc de cercle , est noté P(Q). Comme la plupart des cercles ne sont pas tracés au compas, les points centraux et circonférentiels sont nommés explicitement. L'arc peut également être nommé. Selon le théorème, lorsqu'un cercle tracé au compas est fourni, il est simplement appelé « cercle donné » ou « cercle fourni ». Le cercle fourni doit toujours être supposé être placé arbitrairement dans le plan avec un rayon arbitraire (c'est-à-dire dans position générale).

Les points d'intersection entre n'importe quelle droite et le cercle donné peuvent être trouvés directement. Le théorème de Poncelet-Steiner n'interdit pas le traitement normal des cercles déjà tracés dans le plan ; les règles normales de construction s'appliquent. Le théorème interdit seulement la construction de nouveaux arcs de cercle avec un compas.

Les constructions de Steiner et les constructions ici prouvant le théorème de Poncelet-Steiner nécessitent le placement arbitraire de points dans l'espace. Dans certains paradigmes de construction — comme dans la définition géométrique du nombre constructible — cela peut être interdit. Avec une telle restriction contre le placement de points arbitraires, le cercle unique peut en effet être plus faible que le compas.

Pour prouver les constructions n°4 et n°5 ci-dessus, qui sont incluses ci-dessous, quelques constructions intermédiaires nécessaires sont également expliquées ci-dessous car elles sont utilisées et référencées fréquemment. Ce sont également des constructions à règle uniquement. Toutes les constructions ci-dessous s'appuient sur les constructions de base n°1, n°2, n°3 et sur toute autre construction répertoriée avant elles.

Cette construction ne nécessite pas l’utilisation du cercle donné. Naturellement, toute droite qui passe par le centre du cercle donné a implicitement un segment bissecté : le diamètre est divisé en deux par le centre. Le GIF animé intégré dans l'introduction de cet article démontre cette construction — en s'appuyant sur le diamètre divisé en deux ; l'arc de cercle n'est jamais utilisé — ce qui est réitéré ici sans le cercle et avec des étapes énumérées.

Étant donné une droite arbitraire n (en noir) sur laquelle existent deux points A et B, ayant un milieu M entre eux, et un point arbitraire P dans le plan (supposément hors de la droite n) par laquelle une parallèle à la droite n doit passer :

1. Construire une droite AP (en rouge).
2. Construire une droite BP (en orange).
3. Définir un point arbitraire R sur la droite AP.
4. Construire une droite BR (en vert).
5. Construire une droite MR (en bleu clair).
6. Les droites MR et BP se coupent au point X.
7. Construire une droite AX (en violet).
8. Les droites BR et AX se coupent au point Q.
9. Construire une droite PQ (en bleu foncé), qui est la parallèle souhaitée.

Dans certaines publications, le segment de droite divisé en deux est parfois considéré comme un « cercle » unidimensionnel existant sur la droite. Alternativement, certaines publications considèrent le segment de droite coupé en deux comme un cercle bidimensionnel dans un espace tridimensionnel avec la droite passant par un diamètre, mais non parallèle au plan, coupant ainsi le plan de construction en deux points sur la circonférence, le point médian étant simplement le centre du cercle prescrit.

Cette construction est un cas particulier de la construction du conjugué harmonique, qui n'est pas démontrée dans cet article.

Si la droite passe par le centre d'un cercle, le segment défini par le diamètre passant par le cercle est divisé en deux par le centre du cercle. Dans le cas général, cependant, toute autre droite du plan peut comporter un segment bissecté. Cette construction nécessite l'utilisation du cercle donné.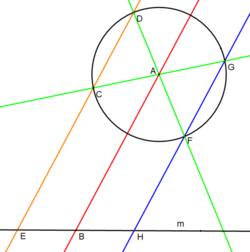

Étant donné une droite, m (en noir), et un cercle centré en A, nous souhaitons créer des points E, B, et H sur la droite telle que B soit le milieu :

1. Tracer une droite arbitraire (en rouge) passant par le centre des cercles donné, A, et le milieu souhaité B (choisi arbitrairement) sur la droite m.
   • Noter que la droite rouge, AB, passe par le centre du cercle et met en évidence un diamètre, divisé en deux par le centre du cercle. Tout parallèle peut être fait à partir de cette droite selon la construction précédente.
2. Choisir un point arbitraire C sur le cercle donné
   • Pour plus de commodité, le point ne doit pas se trouver sur la perpendiculaire de la droite AB passant par le centre du cercle.
3. Construire une droite (en orange), passant par C, parallèle à la droite rouge AB.
   • Si le point C est sur la perpendiculaire de AB passant par le centre du cercle, la parallèle serait une tangente au cercle. La construction est possible par d'autres moyens non listés dans cet article, mais il n'est pas non plus nécessaire de choisir un tel point.
   • Ce parallèle coupe le cercle donné en D.
   • Ce parallèle coupe également la droite noire m en E, définissant une extrémité du segment de droite.
4. Créer deux droites (en vert), AC et AD, qui passent chacune par le centre des cercles donné.
   • Ces droites vertes coupent le cercle donné aux points G et F, respectivement.
5. La droite FG (en bleu) coupe la droite m en H, définissant l'autre extrémité du segment de droite.
   • Le segment EH existe désormais, coïncidant avec la droite m et ayant un point médian B.

Comme le point C est choisi arbitrairement, il n'est pas nécessaire qu'il se trouve sur la perpendiculaire de la droite AB passant par le centre du cercle. Si tel est le cas, la droite CD est simplement la droite tangente au cercle passant par le point C, qui coïncide avec le point D. Cette construction est possible bien que la construction ne soit pas répertoriée dans cet article. Les points F et G peuvent être construits comme auparavant et seront également égaux. Et encore une fois, la droite GF est simplement la droite tangente au cercle en ce point. Ainsi les points E, H et leur milieu B peuvent être trouvés, comme auparavant, avec seulement un changement mineur ajoutant une sous-construction.

Cette construction nécessite l'utilisation du cercle donné. Afin de généraliser la construction de droites parallèles à toutes les droites possibles, pas seulement à celles avec un segment de droite colinéaire bissecté, il devient nécessaire de disposer d'informations supplémentaires. Conformément au théorème de Poncelet-Steiner, un cercle (de centre) est l'objet de choix pour cette construction.

Pour construire une droite parallèle à une droite donnée, passant par n'importe quel point du plan, on combine trivialement deux constructions :

1. Toute droite à partir de laquelle un parallèle doit être établi doit avoir un segment bissecté construit dessus, s'il n'en existe pas déjà un.
2. Une parallèle est alors construite selon la construction de la parallèle précédente impliquant le segment colinéaire bissecté.

Dans des constructions alternatives, qui ne sont pas démontrées dans cet article, une parallèle peut être construite à partir de n'importe quelle paire de droites déjà parallèles l'une à l'autre ; ainsi une troisième parallèle peut être produite à partir de deux droites quelconques, sans utiliser de cercle. De plus, une parallèle à n'importe quelle droite peut être construite chaque fois qu'il existe dans le plan un parallélogramme, également sans l'utilisation d'un cercle donné.

Cette construction nécessite l'utilisation du cercle donné et tire parti du théorème de Thalès.

À partir d'une droite donnée m et d'un point donné A dans le plan, une perpendiculaire à la droite doit être construite passant par le point. Le cercle donné O(r) est fourni.

1. Si la droite souhaitée à partir de laquelle une perpendiculaire doit être créée, m, ne passe pas par le cercle donné — comme illustré — ou si elle passe également par le centre du cercle donné, alors une nouvelle droite parallèle (en rouge) peut être construit arbitrairement de telle sorte qu'il passe par le cercle donné mais pas par son centre, et la perpendiculaire doit plutôt être faite à partir de cette droite.
2. Cette droite rouge qui passe par le cercle donné mais pas par son centre, coupera le cercle donné en deux points, B et C.
3. Tracer une droite BO (en orange), passant par le centre du cercle.
   • Cette droite coupe le cercle donné au point D.
4. Tracer une droite DC (en vert clair).
   • Cette droite est perpendiculaire aux droites rouges (et donc noires), BC et m.
5. Construire un parallèle de la droite DC passant par le point A en utilisant les constructions précédentes.
   • Une perpendiculaire à la droite noire d'origine, m, existe maintenant dans le plan, la droite DC.
   • Une parallèle à n'importe quelle droite par n'importe quel point du plan peut être construite.

Si la droite à partir de laquelle une perpendiculaire doit être tracée passe par le centre du cercle, une approche alternative consisterait à construire les droites tangentes au cercle aux points d'intersection des droites, en utilisant les constructions de Steiner. Ceci n’est pas démontré dans cet article.

Une autre option dans le cas où la droite passe par le centre du cercle serait de lui construire une parallèle passant par le cercle en un point arbitraire. Un trapèze isocèle (ou potentiellement un triangle isocèle) est formé par les points d'intersection du cercle des deux droites, dont les deux côtés non parallèles peuvent être étendus jusqu'à un point d'intersection entre eux et une droite tracée à partir de là passant par le centre du cercle. Cette droite est perpendiculaire et le diamètre est divisé en deux par le centre.

Par une construction alternative non démontrée dans cet article, une perpendiculaire à n'importe quelle droite peut être construite sans cercle, à condition qu'il existe dans le plan un carré.

Étant donné est un segment de droite AB, qui doit être divisé en deux. Facultativement, une droite parallèle m existe dans le plan.

1. Si la droite m, qui est parallèle au segment de droite AB, n'existe pas dans le plan alors elle doit être construit selon des constructions antérieures en utilisant le cercle donné dans le plan (non représenté).
   • Un cercle donné dans le plan n'est pas requis pour cette construction si le parallèle existe déjà.
   • Le parallèle peut être placé arbitrairement dans le plan, à condition qu'il ne soit pas colinéaire avec le segment de droite.
2. Choisir arbitrairement un point C dans le plan qui n'est pas colinéaire avec la droite ou le segment de droite.
   • On peut alternativement construire le point C comme l'intersection des droites AD et BE, à condition que les points D et E existent déjà sur une droite parallèle m.
3. Tracer une droite AC (en rouge), coupant la droite m au point D.
4. Tracer une droite BC (en orange), coupant la droite m au point E.
5. Tracer deux droites, AE et BD (chacune en vert clair), se croisant au point X
6. Tracer une droite CX (en bleu), coupant le segment AB au point M.
   • Le point M est le point médian souhaité du segment AB.
   • La droite CX' coupe également le segment DE

Pour plus de perspective, dans un certain sens, cette construction est une variante d'une construction précédente d'un parallèle à partir d'un segment de droite bissecté, et est donc également un cas particulier du conjugué harmonique projectif (non fourni dans cet article). Il s’agit du même ensemble de droites prises dans leur ensemble, mais construites dans un ordre différent et à partir d’un ensemble initial de conditions différent, pour arriver à un objectif final différent.

Puisque tout segment arbitraire sur l’une des deux droites parallèles peut être divisé en deux, et que toute droite comportant un segment divisé en deux peut avoir un parallèle construit, les deux scénarios sont des propositions géométriquement équivalentes. Ils s’impliquent mutuellement ; une construction simple peut convertir un scénario en un autre sans aucune information supplémentaire.

Dans une construction alternative, tout segment de droite peut être divisé en deux chaque fois qu'un parallélogramme existe dans le plan.

Pour définir un cercle, seul le centre et un point (n'importe quel point) sur la circonférence sont nécessaires. En principe un nouveau point B' est construit tel que le cercle A(B) est égal au cercle A(B'), bien que le point B ne soit pas égal au point B'. Essentiellement, le segment AB tourne autour du point de l'axe A, jusqu'à AB', pour un ensemble différent de points de définition pour le même cercle.

Une façon de procéder qui satisfait la plupart des conditions est la suivante :

1. Dessiner le segment de droite AB (en noir).
2. Construire un parallèle (en rouge) de droite AB passant par le centre, point O, du cercle donné.
   • Le parallèle coupe le cercle donné en un certain point b.
3. Choisir arbitrairement un point b' sur le cercle donné non colinéaire avec la droite Ob.
4. Tracer une droite Ob' (en orange).
5. Construire une droite parallèle à Ob' passant par le point A (en rose).
6. Tracer une droite bb' (en vert clair), reliant les points sur la circonférence des cercles.
7. Construire un parallèle de droite bb' passant par le point B (en bleu).
8. Couper les parallèles bleu et rose, à partir des points B et A, respectivement.
   • C'est le point B'.
   • Le point B' est le point souhaité, faisant pivoter le segment de droite et définissant le même cercle centré en A.

Cette construction échouera si la rotation souhaitée est diamétralement opposée au cercle (c'est-à-dire une rotation en demi-cercle). Une solution à ce scénario consiste à utiliser deux constructions de rotation distinctes, aucune n'étant une rotation en demi-cercle par rapport à la précédente, l'une agissant comme une étape intermédiaire. On choisit alors arbitrairement n'importe quel angle de rotation, on effectue cette première rotation, puis on choisit l'angle supplémentaire et on effectue la rotation une seconde fois.

Il existe une deuxième solution alternative de construction par rotation, basée sur des projections et des points de perspective. Bien qu'il évite la complication de rotation en demi-cercle susmentionnée, il présente ses propres complications, qui sont résolues de la même manière avec des constructions de rotation intermédiaires. La construction n'est pas plus polyvalente. Cela n’est pas démontré dans cet article.

Cette construction nécessite l'utilisation du cercle donné (qui n'est pas représenté) pour les sous-constructions référencées démontrées précédemment.

Supposons que deux cercles A(B) et C(D) soient implicitement donnés, définis uniquement par les points A, B, C et D dans le plan , avec leurs centres définis, mais ne sont pas construits à la boussole. L'axe radical, droite m (en bleu foncé), entre les deux cercles peut être construit :

1. Tracer une droite AC (en orange) passant par les centres des cercles.
2. Tracer un segment de droite BD (en rouge) entre les points sur la circonférence des cercles.
3. Trouver le point médian, M, du segment BD.
4. Tracer des droites AM et CM (toutes deux en vert clair), reliant le milieu du segment avec chacun des centres du cercle.
5. Construire une droite j (en violet) passant par le point B, et perpendiculaire à AM .
   • La droite j est les axes radicaux entre le cercle M(B) et le cercle A(B).
6. Construire une droite k (en vert foncé) passant par le point D, et perpendiculaire à CM' '.
   • La droite k est les axes radicaux entre le cercle M(B) et le cercle C(D).
7. Les droites j et k se coupent au point X.
   • Si les droites j et k sont parallèles alors le milieu du segment M est sur la droite AC — les centres des cercles A(B), C(D) , et M(B) sont colinéaires — et la construction échouera. Une approche alternative est nécessaire (voir ci-dessous).
   • Le point X est le centre radical entre les cercles A(B), C(D), et M(B), et est donc le point unique qui se trouve sur l'axe radical entre deux des trois cercles.
8. Construire une droite m (en bleu foncé) perpendiculaire à la droite AC et passant par le point X.
   • La droite m est l'axe radical souhaité.

Dans le cas où la construction de l'axe radical échoue en raison de l'absence de point d'intersection X entre les droites parallèles j et k, ce qui résulte de la coïncidence du placement du point médian M sur la droite AC, une approche alternative est nécessaire. Une de ces approches consiste à faire pivoter le segment AB autour du point de l'axe A (le centre du cercle A(B)). Une fois arrivée à la rotation arbitraire AB', qui définit le même cercle, la construction de l'axe radical peut recommencer sans problème.

Cette construction nécessite l'utilisation du cercle fourni, O(r). N'importe quelle droite peut être naturellement coupée par n'importe quel cercle tracé par une boussole.

Étant donné la droite M (en noir) et le cercle P(Q), qui n'est pas construit avec une boussole. Les points d'intersection du cercle P(Q) et de la droite M, qui sont le point A et B, peut être construit :

1. Tracer une droite PQ (en rouge) passant par les points définissant le cercle.
   • Si le point O est colinéaire avec la droite PQ alors le segment PQ devra être tourné autour du point central P du cercle, et cette construction recommencera.
2. Construire un parallèle (en orange) de droite PQ passant par le centre O du cercle fourni.
   • Le parallèle coupe le cercle fourni en deux points, dont l'un est arbitrairement choisi : R.
3. Tracer une droite PO (en vert clair), passant par les centres des deux cercles (c'est-à-dire celui fourni par la construction de la boussole et celui qui doit être intersecté ).
4. Tracer une droite QR (en bleu clair), reliant les deux points sur les circonférences des deux cercles.
5. Couper les droites PO et QR au point X.
   • Si le point X n'existe pas à cause des droites PO et QR étant parallèle - ce qui résulte de cercles P(Q) et O(r) ayant des rayons égaux - puis revenir à l'étape 2 et choisir l'autre point d'intersection, R.
6. En choisissant arbitrairement un point M sur la droite m, tel qu'il ne soit pas sur la droite PO, tracer une droite PM (en rose).
   • Pour simplifier la construction et seulement si la droite PQ n'est pas parallèle à la droite m, les droites PM et PQ peuvent coïncider.
7. Tracer une droite MX (en marron).
8. Construire une parallèle (en violet foncé) de droite PM passant par le centre O du cercle fourni.
   • La parallèle coupe la droite MX en un point N.
9. Construire un parallèle (en jaune) de droite m passant par le point N.
   • La parallèle coupe le cercle fourni aux points C et D.
   • Si la parallèle ne coupe pas le cercle fourni, alors la droite m ne coupe pas non plus le cercle P(Q).
10. Tracer des droites CX et DX (toutes deux en bleu foncé).
    • Ces droites coupent toutes deux la droite m aux points A et B, respectivement.
11. Les points A et B sont les points d'intersection souhaités entre la droite m et le cercle P(Q).

L’intersection entre deux cercles devient une combinaison triviale de deux constructions antérieures :

1. Construire l'axe radical entre les deux cercles.
2. Construire les points d'intersection entre l'axe radical et l'un ou l'autre des deux cercles arbitrairement choisis :
   • L'axe radical est une droite, donc cette construction est possible selon la construction construction de base n^o 4.
3. Ces points sont les points d'intersection souhaités des cercles.
   • Les deux cercles et l'axe radical se coupent tous aux mêmes lieux de points : deux points, un point s'ils sont tangents, ou aucun s'ils ne se coupent pas.
   • Si l'axe radical ne coupe pas un cercle, alors il ne coupe ni l'un ni l'autre, et les deux cercles ne se coupent pas non plus.

La deuxième construction de base – décrivant un cercle complet avec seulement deux points de définition – n'a jamais nécessité la construction d'un arc avec le compas pour que le cercle puisse être utilisé dans les constructions. À savoir, les intersections de cercles avec des cercles et avec des droites, qui constituent ensemble l'essence de toutes les constructions impliquant un cercle, sont réalisables sans arc. Ainsi, définir un cercle par son centre et par tout point arbitraire sur sa circonférence est suffisant pour décrire complètement le cercle entier et construire avec lui. En tant que tel, l’arc n’a qu’un objectif esthétique. La construction de base n^o 2 est satisfaite.

Bien qu'il s'agisse d'un sujet distinct en soi, de nombreux concepts de « géométrie projective » sont appliqués ici aux constructions de Steiner. Jean-Victor Poncelet fut un contributeur majeur sur le sujet lorsqu'il postula le théorème de cet article, que Jakob Steiner démontra plus tard. De nombreux concepts connexes développés en géométrie projective incluent, sans s'y limiter : la concurrence, les "points à l'infini", la perspective, les rapports et les rapports croisés, les points stables ou fixes d'involutions, les invariants, l'homogénéité, les transformations linéaires, les harmoniques projectives et autres. Un traitement approfondi des constructions de Steiner et de leurs preuves nécessite une formation en géométrie projective, bien que le sujet de la géométrie projective ne se limite pas aux constructions à la règle uniquement.

Le théorème de Poncelet-Steiner peut être comparé au théorème de Mohr-Mascheroni, qui stipule que toute construction à la règle et au compas peut être réalisée avec seulement un compas. La règle n'est pas nécessaire mais à des fins esthétiques ; rien d'autre n'est nécessaire dans le plan.

La restriction du compas rouillé autorise l'utilisation d'un compas et d'une règle, à condition que le compas produise des cercles de rayon fixe. Bien que les constructions au compas rouillé aient été explorées depuis le X^e siècle et qu'il ait été démontré que tout Euclide était constructible avec un compas rouillé au XVII^e siècle, le théorème de Poncelet-Steiner prouve que le compas rouillé et la règle ensemble sont plus que suffisantes pour tout et toute construction euclidienne. En effet, le compas rouillé devient un outil simplifiant les constructions au-delà de la simple règle et du simple cercle. Vu d’un autre côté, le théorème de Poncelet-Steiner fixe non seulement l'écartement du compas rouillé, mais garantit que le compas se brise après sa première utilisation.

Le théorème d'équivalence du compas (en) prouve que le compas rigide (également appelé compas moderne) — celui qui maintient son espacement lorsqu'il est soulevé du plan — est équivalent au compas pliable traditionnel (également appelé diviseur) — celui qui ne retient pas son écartement, se "remettant ainsi à zéro", à chaque fois qu'il est soulevé du plan. La capacité de transférer des distances (c'est-à-dire de construire des cercles congruents) — une opération rendue triviale par le compas rouillé — a été prouvée par Euclide comme étant possible avec le compas qui se referme. En fait, cela peut être fait en utilisant uniquement le compas repliable, sans la règle. Par conséquent le compas rigide et le compas repliable sont équivalents ; ce qui peut être construit par l’un peut être construit par l’autre.

L'exigence imposée au théorème de Poncelet-Steiner - qu'un cercle avec son centre fourni existe dans le plan - a depuis été généralisée, ou renforcée, pour inclure des conditions alternatives mais tout aussi restrictives.

Il existe sans aucun doute d’autres scénarios uniques que ceux énumérés ici. Il ne s’agit pas d’une liste exhaustive de possibilités.

Dans une telle alternative, le cercle entier n’est pas du tout requis. En 1904, Francesco Severi prouva que n'importe quel petit arc (du cercle), accompagné du centre, suffisait^[4]. Cette construction brise le compas rouillé à tout moment avant que le premier cercle ne soit terminé, mais après qu'il a commencé, dessinant ainsi une partie continue de l'arc de cercle dans le plan, et toutes les constructions restent néanmoins possibles. Ainsi, les conditions faisant l'hypothèse du théorème de Poncelet-Steiner peuvent effectivement être affaiblies, mais uniquement par rapport à l'exhaustivité de l'arc de cercle, et non, selon le théorème de Steiner, par rapport au centre.

Le théorème démontre la construction de Steiner des points d'intersection entre une droite et le cercle d'un arc, quelle que soit la taille ou la position de l'arc, en utilisant uniquement une règle et l'arc. La construction, également, n'utilise pas le centre du cercle de l'arc. Bien que le centre soit nécessaire pour compléter l'ensemble d'Euclide, comme le prouvent tous deux le théorème de Steiner et le théorème de Poncelet-Steiner, le centre n'est pas nécessaire pour couper une droite avec le cercle de cet arc. En utilisant cette construction, l'arc et le centre du cercle de l'arc, toutes les constructions Poncelet-Steiner ci-dessus sont également réalisables, quoique avec plus de difficulté.

Dans deux autres variantes, le centre peut être entièrement omis à condition qu'il s'agisse soit de deux cercles concentriques, soit de deux cercles distincts sécants, dont il existe deux cas : deux points d'intersection et un point d'intersection (cercles tangentiels). À partir de n'importe lequel de ces scénarios, des centres peuvent être construits, réduisant le scénario à l’hypothèse initiale. Ceci ne contredit pas le théorème de Steiner qui, bien qu'il affirme qu'un centre est absolument requis, émet également l'hypothèse qu'un seul cercle existe.

Il existe encore d'autres variantes. Il suffit d'avoir deux cercles non sécants et non concentriques (sans leurs centres), à condition qu'au moins un point soit donné soit sur la droite médiane qui les traverse, soit sur l'axe radical qui les sépare, ou à condition que deux droites parallèles arbitrairement dans le plan. Il suffit également, alternativement, d'avoir trois cercles qui ne se croisent pas^[5]. Une fois qu'un seul centre est construit, le scénario se réduit à nouveau à l'hypothèse originale du théorème de Poncelet-Steiner.

Dans chacun de ces scénarios, il existe plus d’informations qu’un simple deuxième cercle. Le fait que deux cercles soient concentriques, ou que deux cercles aient des points d'intersection connus, ou la présence d'un troisième cercle, ou d'un point soit sur une droite médiane, soit sur un axe radical, constitue une information supplémentaire au-delà de la simple présence d'un deuxième cercle.

De plus, dans chacun des scénarios mentionnés précédemment, l'exhaustivité de l'arc de cercle n'est pas nécessaire, conformément au théorème de Severi de 1904, à condition que les intersections de cercles soient explicitement données chaque fois que les arcs de cercle n'existent pas là où les points d'intersection existent. Autrement dit, si les points d'intersection ne peuvent pas être trouvés directement à travers les deux arcs, ils doivent être fournis. L’intégralité de l’arc de cercle est par ailleurs redondante.

Au lieu de restreindre davantage les règles de construction, il est tout aussi intéressant d’étudier l’assouplissement de ces restrictions. Celles-ci sont parfois appelées « constructions étendues », car elles étendent ce qui est constructible en étendant l'ensemble d'outils autorisé. Ces constructions sont également appelées « neusis » (du grec) car elles emploient d'autres outils que le compas et la règle, ou « constructions libérées » car elles atténuent les restrictions du paradigme traditionnel.

Tout comme les géomètres ont étudié ce qui reste possible de construire (et comment) lorsque des restrictions supplémentaires sont imposées aux règles de construction traditionnelles - comme le compas uniquement, la règle uniquement, le compas rouillé, etc. - ils ont également étudié quelles constructions deviennent possibles qui ne l'étaient pas. déjà lorsque les restrictions naturelles inhérentes aux règles de construction traditionnelles sont allégées. Des questions telles que « qu'est-ce qui devient constructible », « comment pourrait-il être construit », « quelles sont les règles traditionnelles à enfreindre le moins possible », « quels sont les outils les plus simples nécessaires », « quels outils apparemment différents sont équivalents », etc. demandé.

Un angle arbitraire est non trisectable en utilisant les règles traditionnelles du compas et de la règle, par exemple, mais la trisection devient constructible lorsqu'on lui permet l'outil supplémentaire d'une ellipse dans le plan, qui n'est lui-même pas constructible. Certains des problèmes traditionnels non résolus tels que la trisection d'angle, la duplication du cube, la quadrature du cercle, la recherche de racines cubiques, etc., qui se sont révélés impossibles à l'aide d'une règle et d'un compas seuls, ont été résolus à l'aide d'un ensemble d’outils élargi. En général, les objets étudiés pour élargir le champ de ce qui est constructible comprennent :

• Courbes "auxiliaires" non constructibles dans le plan — y compris les coniques, les cycloïdes, les lemniscates, les limaçons, les spirales d'Archimède, les spirales d'Euler, n'importe laquelle des trissectrices ou quadratrices (en), et autres.
• Des outils physiques autres que le compas et la règle — généralement appelés neuseis — qui comprennent des outils spécifiques tels que le trisecteur de Bergery, des règles marquables et à double tranchant, des règles graduées, règles triangulaires droites, liaison, ellipsographe, pistolets et autres.
• Mathématiques des origamis (l'étude mathématique et géométrique de l'origami).

Les géomètres anciens considéraient les constructions au compas et à la règle (connues sous le nom de « constructions planaires ») comme idéales et préférées. Deuxièmement, ils ont préféré les constructions solides, qui incluaient l'utilisation de coniques dans un plan autre que le cercle. Ils ont favorisé en troisième lieu l'utilisation de courbes lisses arbitraires dans le plan, et encore moins l'utilisation de neuseis (outils physiques portables alternatifs). Il est peu probable que les géomètres anciens — du moins ceux du monde occidental — aient même envisagé le pliage du papier.

Le terme « neusis » peut également faire référence à un outil ou une méthode spécifique employé par les géomètres anciens.

Il convient de souligner que dans tous les paradigmes de construction, la règle implicite est que toutes les constructions doivent se terminer par un nombre fini d'applications des outils disponibles (compas et règle) et produire exactement les résultats escomptés. Des discussions entières pourraient avoir lieu sans l’une ou l’autre de ces conditions.

Pour toute figure autrement non constructible :

• Il est possible d'approcher une construction à un niveau prédéterminé de précision en utilisant uniquement un compas et une règle, en utilisant une approche réitérative.
• Une construction exacte peut devenir possible à la limite infinie de ce processus convergent, mais nécessite des constructions infinies.

Par exemple, une trisection d'angle peut être réalisée exactement en utilisant une séquence infinie de bissections d'angle. Si la construction se termine à une itération finie, une approximation précise d'une trisection peut être obtenue avec une précision arbitraire. Bien que chaque point, droite ou cercle soit une construction valable, ce qu’il vise à approcher ne peut jamais être véritablement réalisé.

Il existe bien sûr des figures exactement constructibles qui sont des approximations raisonnables de figures non constructibles, comme des constructions non itératives relativement simples pour une approximation de l'heptagone.

• Carré de charpentier (en)
• Polygone constructible
• Inversion
• Géométrographie (en)
• Axiomes de Huzita-Hatori (en)
• Grand théorème de Poncelet

• (en) Howard Eves, A Survey of Geometry /Volume one, Allyn and Bacon, 1963
• (en) Merlyn Retz et Meta Darlene Keihn, Historical Topics for the Mathematics Classroom, National Council of Teachers of Mathematics (NCTM), 1989, 192–196 p. (ISBN 9780873532815)

• (en) Howard Whitley Eves, College Geometry, Jones & Bartlett Learning, 1995, 180–186 p. (ISBN 9780867204759, lire en ligne)
• (de) Jacob Steiner, Die geometrischen Konstructionen, ausgeführt mittelst der geraden Linie und eines festen Kreises, als Lehrgegenstand auf höheren Unterrichts-Anstalten und zur praktischen Benutzung, Berlin, Ferdinand Dümmler, 1833 (lire en ligne)
• (en) A. S. Smogorzhevskii, The Ruler In Geometrical Constructions (Popular Lectures In Mathematics Vol. 5), 1961 (lire en ligne)

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Poncelet–Steiner theorem » (voir la liste des auteurs).
• (en) Jacob Steiner's theorem sur cut-the-knot (il est impossible de trouver le centre d'un cercle à la règle seule)
• (en) Arseniy Akopyan et Roman Fedorov, « Two circles and only a straightedge », Proceedings of the AMS, vol. 147, n^o 1,‎ 2019, p. 91-102 (arXiv abs/1709.02562)
• (en) Christian Gram, « A remark on the construction of the centre of a circle by means of the ruler », Mathematica Scandinavica, vol. 4, n^o 1,‎ 1956, p. 157-160 (JSTOR 24490022, lire en ligne)
• (en) Štefan Porubský, « Poncelet-Steiner Theorem », sur Interactive Information Portal for Algorithmic Mathematics
• (en) « Poncelet-Steiner Theorem » [PDF]
• (en) A. S. Smogorzhevskii, The Ruler in Geometrical Constructions, 1961 (lire en ligne)

• Portail de la géométrie