|
Lewis Fry Richardson Lewis Fry Richardson (Newcastle upon Tyne, 11 ottobre 1881 – Kilmun, 30 settembre 1953) è stato un matematico, fisico, meteorologo, psicologo e pacifista britannico, famoso per aver aperto la strada ai moderni metodi matematici di previsione meteorologica e per aver cercato di applicare tecniche simili allo studio delle cause delle guerre allo scopo di prevenirle. È anche noto per il suo lavoro pionieristico sui frattali e per un metodo per risolvere un sistema di equazioni lineari noto come iterazione di Richardson modificata.[1] BiografiaLewis Fry Richardson era il più giovane di sette figli nati da Catherine Fry (1838-1919) e David Richardson (1835-1913). Si trattava di una prospera famiglia quacchera, con il padre che gestiva una fiorente attività di concia e produzione di pelli.[2] All'età di 12 anni fu mandato in un collegio quacchero, la Bootham School[3][4] a York, dove ricevette un'istruzione scientifica, che stimolò in lui un attivo interesse per la storia naturale . Nel 1898 si iscrisse al Durham College of Science (facente parte della Durham University) dove seguì corsi di fisica matematica, chimica, botanica e zoologia. Nel 1900 proseguì gli studi al King's College di Cambridge, dove ebbe come professore di fisica Joseph John Thomson e ottenne la laurea di primo livello nel 1903.[5] All'età di 47 anni conseguì inoltre un dottorato in psicologia matematica presso l'Università di Londra.[6] Gli interessi eclettici di Richardson si rifletterono in una vita lavorativa molto variegata:[7]
Nel 1926 fu nominato membro della Royal Society[8] Vita privataNel 1909 sposò Dorothy Garnett (1885-1956), figlia del matematico e fisico William Garnett.[9] Non potevano avere figli a causa di un'incompatibilità dei gruppi sanguigni, ma adottarono due figli e una figlia tra il 1920 e il 1927.[10] Il nipote di Richardson, Ralph Richardson, divenne un attore famoso. Il suo pronipote (attraverso il fratello maggiore di sua moglie Dorothy, (James Clerk) Maxwell Garnett, C.B.E.), Julian Hunt, diventò un meteorologo e fu direttore generale e amministratore delegato del British Meteorological Office dal 1992 al 1997.[11] Una pronipote, della stessa discendenza, è l'ex politica Virginia Bottomley, ora baronessa Bottomley.[12][13] PacifismoLe convinzioni quacchere di Richardson implicavano un ardente pacifismo che lo esonerava dal servizio militare durante la prima guerra mondiale in quanto obiettore di coscienza, anche se questo successivamente lo squalificò da qualsiasi incarico accademico. Richardson lavorò dal 1916 al 1919 per la Friends' Ambulance Unit, che operava nella 16ª divisione di fanteria francese. Dopo la guerra, tornò all'Ufficio meteorologico, ma fu costretto a dimettersi a causa della sua obiezione di coscienza quando fu unito al Ministero dell'Aria nel 1920. Successivamente intraprese una carriera ai margini del mondo accademico, prima di ritirarsi nel 1940 per ricercare le proprie idee. Il suo pacifismo ebbe conseguenze dirette sui suoi interessi di ricerca. Secondo Thomas Körner,[14] la scoperta che i suoi lavori di meteorologia suscitavano l'interesse dei progettisti di armi chimiche lo indusse ad abbandonare tutti i suoi sforzi in questo campo e a distruggere le scoperte che doveva ancora pubblicare. Previsioni del tempoL'interesse di Richardson per la meteorologia lo portò a ipotizzare la risoluzione di equazioni differenziali come metodo per ricavare le previsioni meteorologiche, l'approccio utilizzato oggi, sebbene quando pubblicò Weather Prediction by Numerical Process nel 1922, non esisteva ancora un modo per svolgere calcoli in maniera sufficientemente veloce. Quando, nel 1950, Richardson ricevette la notizia delle prime previsioni meteorologiche svolte sul primo computer moderno, ENIAC, egli rispose che i risultati costituivano un "enorme progresso scientifico". I primi calcoli svolti da ENIAC per una previsione di 24 ore impiegarono quasi 24 ore per essere completati.[15] Egli si interessò anche alla turbolenza atmosferica ed eseguì molti esperimenti terrestri. Il numero di Richardson, un parametro adimensionale usato nella teoria della turbolenza, è chiamato così in suo onore. Riassunse notoriamente la turbolenza in versi in rima in Weather Prediction by Numerical Process (p 66):[16]
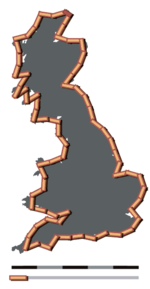
[Un gioco di parole su Siphonaptera, la riformulazione del concetto di Jonathan Swift da parte di Augustus De Morgan, "Le grandi pulci hanno piccole pulci sulla schiena che le mordono, e le piccole pulci hanno pulci minori, e così all'infinito." (A Budget of Paradoxes, 1915)]. Tali versi costituiscono la prima descrizione del concetto di cascata di energia, cruciale nelle descrizioni statistiche dei moti turbolenti. Il tentativo di Richardson di previsione numericaUno dei risultati più celebri di Richardson è il suo tentativo di prevedere il tempo retroattivamente durante un solo giorno, il 20 maggio 1910, mediante calcoli diretti. A quel tempo, i meteorologi eseguivano le previsioni principalmente cercando andamenti meteorologici simili da registrazioni passate, procedendo con estrapolazioni. Richardson tentò di utilizzare un modello matematico che descrivesse le principali caratteristiche dell'atmosfera e di utilizzare i dati rilevati in un momento specifico (7 del mattino) per calcolare il tempo sei ore dopo ab initio. Come spiega il meteorologo Peter Lynch,[17] la previsione di Richardson fallì in modo drammatico, prevedendo un enorme aumento della pressione (145 hPa) in sei ore quando essa rimase effettivamente più o meno statica. Tuttavia, un'analisi dettagliata di Lynch dimostrò che la causa era semplicemente la mancata applicazione di tecniche di regolarizzazione dei dati, che rimuovono picchi di pressione non fisici. Quando esse vengono applicate, la previsione di Richardson si rivela sostanzialmente accurata: un risultato notevole, considerando che i calcoli furono eseguiti a mano e oltretutto mentre prestava servizio con l'unità di ambulanza quacchera nel nord della Francia. Analisi matematica della guerraRichardson applicò inoltre le sue abilità matematiche al servizio dei suoi principi pacifisti, in particolare nella comprensione delle cause dei conflitti internazionali. Per questo motivo, al giorno d'oggi è considerato l'iniziatore, o co-iniziatore (con Quincy Wright e Pitirim Sorokin e altri come Kenneth Boulding, Anatol Rapaport e Adam Curle), dell'analisi scientifica del conflitto, un argomento interdisciplinare delle scienze sociali matematiche dedicato all'indagine sistematica delle cause della guerra e delle condizioni di pace. Come aveva fatto con il tempo meteorologico, analizzò la guerra usando principalmente equazioni differenziali e la teoria della probabilità. Considerando gli armamenti di due nazioni, Richardson ipotizzò un sistema idealizzato di equazioni, in base al quale il tasso di accumulo di armamenti di una nazione è direttamente proporzionale alla quantità di armi della sua nazione rivale e anche alle lamentele sentite nei confronti del rivale, e proporzionale in modo negativo al quantitativo di armi che ha possiede. La soluzione di questo sistema di equazioni consente di trarre conclusioni interessanti sulla natura, e sulla stabilità o instabilità, di varie condizioni ipotetiche che potrebbero verificarsi tra le nazioni. Diede anche origine alla teoria che la propensione alla guerra tra due nazioni fosse funzione della lunghezza del loro confine comune. IN Arms and Insecurity (1949) e Statistics of Deadly Quarrels (1960), cercò di analizzare in modo statistico le cause della guerra. I fattori che valutò includevano economia, lingua e religione. Nella prefazione di quest'ultimo scrisse: "C'è nel mondo una grande discussione politica brillante e arguta che non porta a convinzioni definitive. Il mio obiettivo è stato differente: cioè esaminare alcune nozioni con tecniche quantitative nella speranza di raggiungere una conclusione affidabile ". In Statistics of Deadly Quarrels Richardson presentò dati su praticamente ogni guerra dal 1815 al 1945. Di conseguenza, ipotizzò una scala logaritmica in base 10 per i conflitti. In altre parole, ci sono molte più piccoli conflitti, in cui muoiono solo poche persone, rispetto a quelli grandi che ne uccidono molte. Sebbene non sia possibile prevedere in anticipo la dimensione di un conflitto, anzi, è impossibile dare un limite superiore alla serie, nel complesso formano una distribuzione di Poisson. Su scala minore mostrò lo stesso schema per gli omicidi di gruppo a Chicago e Shanghai. Altri hanno notato che modelli statistici simili si verificano frequentemente, sia pianificati (ad esempio le lotterie, con molte più vincite piccole che grandi), o per organizzazione naturale (ci sono più cittadine con negozi di alimentari che grandi città con centri commerciali). Ricerca sulla lunghezza delle coste e dei confiniRichardson decise di cercare una relazione tra la probabilità che due paesi confinanti entrino in guerra e la lunghezza del loro confine comune. Tuttavia, durante la raccolta dei dati, scoprì che c'era una notevole variazione nei valori di lunghezza dei confini fra le varie fonti. Ad esempio, quello tra la Spagna e il Portogallo era variamente citato come 987 o 1214 km, e quello tra Paesi Bassi e Belgio come 380 o 449 km.[18] La ragione di queste incongruenze è il "paradosso della linea costiera". Supponiamo che la costa della Gran Bretagna venga misurata usando una riga di 200 km, specificando che entrambe le estremità del righello devono toccare la costa. A questo punto si taglia la riga a metà e si rifà la misurazione, e così via: Si nota che più piccolo è il righello, più lunga è la costa risultante. Si potrebbe supporre che questi valori convergano a un numero finito che rappresenta la vera lunghezza della costa. Tuttavia, Richardson dimostrò che così non era: la lunghezza misurata delle coste, e di altre curve naturali, aumenta senza limiti man mano che l'unità di misura viene ridotta.[19] Questo fatto è noto al giorno d'oggi come effetto Richardson.[20] A quel tempo, la ricerca di Richardson fu ignorata dalla comunità scientifica. Oggi è invece considerata uno dei primi elementi nello studio moderno dei frattali. La ricerca di Richardson fu citata dal matematico Benoît Mandelbrot nel suo articolo del 1967 How Long Is the Coast of Britain? Richardson identificò un valore (compreso tra 1 e 2) che descriverebbe i cambiamenti (all'aumentare della precisione nella misura) nella complessità osservata per una particolare costa; questo valore servì da modello per il moderno concetto di dimensione frattale.[21] EreditàDal 1997, la Lewis Fry Richardson Medal viene assegnata dalla European Geosciences Union per "contributi eccezionali alla geofisica non lineare in generale" (dalla EGS fino al 2003[22] e dalla EGU dal 2004).[23] I vincitori sono stati:
Dal 1959 esiste un centro di studi sulla pace presso la Lancaster University denominato Richardson Institute, che svolge ricerche interdisciplinari su pace e conflitti nello spirito di Lewis Fry Richardson.[25] Note
Bibliografia
Voci correlateAltri progetti
Collegamenti esterni
|