CIE1931色空間 (シーアイイー 1931 いろくうかん) あるいはCIE1931表色系 (シーアイイー 1931 ひょうしょくけい) は、可視光 と人の色覚 における色 との関係を初めて定量的に表した色空間 である。1931年に国際照明委員会 (CIE)により定義された。CIE1931色空間によって定義される数学的な関係式は、現代のカラーマネージメント に欠かせないツールであり、印刷 用インキ ・トナー やディスプレイ 、デジタルカメラ などの記録装置 を扱う場合において非常に重要な情報になっている。
CIEは1931年にCIE 1931 RGB色空間 、及びCIE 1931 XYZ色空間 の2つの色空間を採択した。[ 1] [ 2] ウィリアム・デビッド・ライト [ 3] [ 4] 分光視感効率
V
(
λ
)
{\displaystyle V(\lambda )}
CIEは、その後もカラーモデルを発展させ続けている。1976年には、XYZ色空間から派生させた、人の知覚に対してより均等に色を数値で表すCIELUV とCIELAB を採択した。近年ではCIECAM02 (英語版 ) 色の見えモデル も発展させている。しかし、CIE 1931 色空間は、現在でも世界標準として広く使用され続けている。
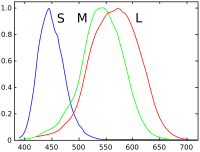
人の錐体細胞における正規化された短、中、長波長の分光感度 (英語版 ) 正常色覚の人では、網膜にある錐体細胞 はその分光感度によって3種類に分類される。短波長(Short)に感度のピークを持つS錐体 、中波長(Medium)に感度のピークを持つM錐体 、長波長(Long)に感度のピークを持つL錐体 である。感度のピークはS錐体が440nm付近、M錐体が540nm付近、L錐体が560nm付近とされる。また、その視物質の吸光波長のピークについては、S錐体が420nm、M錐体が530nm、L錐体が560nmにあるとされる[ 5] 色覚 が生じる。
物理的な光とは分光強度分布 (英語版 ) 原刺激 (原色)と、その数量である三刺激値 (さんしげきち、英 : tristimulus values )と呼ばれる3つの数量で色は表すことができるようになる。色空間によって原刺激と三刺激値はさまざまな種類が考えられるが、たとえば3種類の錐体の単色光に対する反応値の総和を求めることで、三刺激値が得られ、この三刺激値で色を表現できる。この場合、S、M、Lという3つのパラメータによりつくられるLMS色空間 というものになる。LMS色空間は人の色覚を表現するために考案された色空間のうちの一つである。
色空間は、物理的なエネルギーとしての光を、三刺激値といった色を表す客観的な表現に置き換えるものである。必ずしもLMS色空間のように錐体の反応値を直接表すとは限らない。三刺激値に基づく色空間は、3色による加法混色モデルにおける三原色 の総和を概念化したものと関連づけられている。LMS色空間やXYZ色空間のような一部の色空間においては、各々の原色は現実の色としては存在しない虚色 であり、どんな単色光 をつかっても実現させることはできない。
CIE XYZ色空間は、平均的な人が知覚することができるすべての色を包含している。 このため三刺激値によるCIE XYZ色空間はデバイス非依存の色表現である[ 6]
様々な異なる波長が混合された二つの光源について考える。そのような光源は同じ色として認識されることがある。これを条件等色
ほとんどの波長においては、錐体の分光感度においてS, M, Lそれぞれのカーブが相互に重なっているため、二種類あるいは三種類の錐体が刺激される。このため、一つの三刺激値のみを表すことは物理的に不可能である(例として、LMS三刺激値におけるM成分がゼロでない時、L成分もS成分もゼロにはなり得ない)。さらには、LMS三刺激値において、三原色の加法混色の色空間(例えばRGB色空間 )では、単波長の色は少なくとも三色のうち一色は負の値になる。これは、三原色により定義される三角形の外側に色度が位置しているためである。このような負の値をもつRGB値を避けるため、および一つの成分が明所視標準分光視感効率
V
(
λ
)
{\displaystyle V(\lambda )}
虚色 英 : imaginary color )と呼ぶ。
X , Y , Z 代表的なM錐体細胞の正規化されたカーブと、明所視での標準観察者によるCIE 1924分光視感効率曲線の比較。 CIE 1931モデルにおいて、Y Z X § CIE XYZ色空間の定義 を参照)。Y Y XZ 色度 を確認することができる。
X, Y, Z Y = 1Y = 100Y 相対輝度 となる。X, Z 標準光源 から特定することができる。
1950年台に錐体細胞の特性が解明されるよりも遥か以前に、XYZ XYZ
[
X
Y
Z
]
=
[
1
.910
20
−
1
.112
12
0
.201
91
0
.370
95
0
.629
05
0
0
0
1
.000
00
]
[
L
M
S
]
H
P
E
{\displaystyle {\begin{bmatrix}X\\Y\\Z\end{bmatrix}}=\left[{\begin{aligned}1&.910\,20\!\!\!&\!\!-1&.112\,12\!\!\!&\!\!0&.201\,91\\0&.370\,95\!\!\!&\!\!0&.629\,05\!\!\!&\!\!0&\\0&\!\!\!&\!\!0&\!\!\!&\!\!1&.000\,00\end{aligned}}\right]{\begin{bmatrix}L\\M\\S\end{bmatrix}}_{\rm {HPE}}}
異なる定義としては、Zの値はS錐体の反応から定義されており、Yの値はLおよびM錐体の反応を混合したもので、Xの値はLMSの3つの錐体全ての混合であると言える。すなわち、XYZの値はヒトのLMS錐体細胞の感度にある程度類似するよう定義されているが、LMS錐体細胞の感度とは異なるものである。
三刺激値は、目の中の錐体細胞の分布状況により、観察者の視野 に依存し変動してしまう。この依存性を排除するため、CIEは測色標準観察者 を定義し、中心窩 から2度の視野角で得られるヒトの標準的な色覚を定義した。この2度という角度は、中心窩から2度以内の場所に、色を知覚する錐体細胞が分布していると考えられていることから定義されている。このCIE 1931 測色標準観察者はCIE 1931 2度測色標準観察者とも呼ばれている。また、より新しい測色標準観察者として、CIE 1964 10度測色標準観察者が、スタイルズ、バーチ[ 7] [ 8]
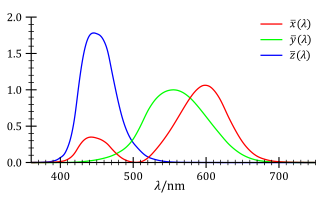
この10度視野角での実験では、観察者は中央から2度の範囲内は無視することにより実験が行われた。このCIE 1964 測色補助標準観測者は、4度以上の視野角での利用に推奨される。これらの測色標準観察者は両方とも、380 nm ~ 780 nm の波長域で 5 nm の離散化で行った上でCIEから配布されている。全て実験から得られたデータは補間 されて計算されている。測色標準観察者は三つの等色関数により特徴づけられている 。
CIE XYZ等色関数、
x
¯
(
λ
)
{\displaystyle {\overline {x}}(\lambda )}
y
¯
(
λ
)
{\displaystyle {\overline {y}}(\lambda )}
z
¯
(
λ
)
{\displaystyle {\overline {z}}(\lambda )}
CIE RGB等色関数、
r
¯
(
λ
)
{\displaystyle {\overline {r}}(\lambda )}
g
¯
(
λ
)
{\displaystyle {\overline {g}}(\lambda )}
b
¯
(
λ
)
{\displaystyle {\overline {b}}(\lambda )}
CIE等色関数
x
¯
(
λ
)
{\displaystyle {\overline {x}}(\lambda )}
y
¯
(
λ
)
{\displaystyle {\overline {y}}(\lambda )}
z
¯
(
λ
)
{\displaystyle {\overline {z}}(\lambda )}
[ 9]
ルックアップテーブル を用いた出力値の特定は、時にテーブルが巨大になり、実装が難しくなる。このためCIE XYZ等色関数はガウス関数 による下記のような近似が可能である[ 10]
g (x ) を区分ガウス関数とすると、
g
(
x
;
μ
,
σ
1
,
σ
2
)
=
{
exp
(
−
1
2
(
x
−
μ
)
2
/
σ
1
2
)
,
x
<
μ
,
exp
(
−
1
2
(
x
−
μ
)
2
/
σ
2
2
)
,
x
≥
μ
.
{\displaystyle g(x;\mu ,\sigma _{1},\sigma _{2})={\begin{cases}\exp {\bigl (}{-{\tfrac {1}{2}}(x-\mu )^{2}/\sigma _{1}^{2}}{\bigr )},&x<\mu ,\\[2mu]\exp {\bigl (}{-{\tfrac {1}{2}}(x-\mu )^{2}/\sigma _{2}^{2}}{\bigr )},&x\geq \mu .\end{cases}}}
ここで、g (x ) は頂点がx = μ σ 1 が頂点から左側の曲線の広がりを表し、σ 2 が右側の広がりを表す。ナノメートル 単位で計測された波長λ を用いて、CIE 1931等色関数は下記のように近似できる。
x
¯
(
λ
)
=
1.056
g
(
λ
;
599.8
,
37.9
,
31.0
)
+
0.362
g
(
λ
;
442.0
,
16.0
,
26.7
)
−
0.065
g
(
λ
;
501.1
,
20.4
,
26.2
)
,
y
¯
(
λ
)
=
0.821
g
(
λ
;
568.8
,
46.9
,
40.5
)
+
0.286
g
(
λ
;
530.9
,
16.3
,
31.1
)
,
z
¯
(
λ
)
=
1.217
g
(
λ
;
437.0
,
11.8
,
36.0
)
+
0.681
g
(
λ
;
459.0
,
26.0
,
13.8
)
.
{\displaystyle {\begin{aligned}{\overline {x}}(\lambda )&=1.056g(\lambda ;599.8,37.9,31.0)+0.362g(\lambda ;442.0,16.0,26.7)\\[2mu]&\quad -0.065g(\lambda ;501.1,20.4,26.2),\\[5mu]{\overline {y}}(\lambda )&=0.821g(\lambda ;568.8,46.9,40.5)+0.286g(\lambda ;530.9,16.3,31.1),\\[5mu]{\overline {z}}(\lambda )&=1.217g(\lambda ;437.0,11.8,36.0)+0.681g(\lambda ;459.0,26.0,13.8).\end{aligned}}}
頂点から左右に分割を行わず、一つのガウス関数で近似をすることも可能である。実際CIE 1964では一つのガウス関数を用いている[ 10]
CIE XYZ等色関数では正の値のみが使われ、全ての色は正のXYZ座標で表現される。その他の、例えばCIE RGB色空間やその他のRGB色空間のような測色標準観察者は、異なる三つの等色関数により定義され、それぞれの値は負の値も含む。よってそれぞれの色空間では負の座標を含む。
この三刺激値は、測色標準観察者における色の分光放射輝度 L e,Ω,λ を用いて:
X
=
∫
λ
L
e
,
Ω
,
λ
(
λ
)
x
¯
(
λ
)
d
λ
,
Y
=
∫
λ
L
e
,
Ω
,
λ
(
λ
)
y
¯
(
λ
)
d
λ
,
Z
=
∫
λ
L
e
,
Ω
,
λ
(
λ
)
z
¯
(
λ
)
d
λ
.
{\displaystyle {\begin{aligned}X&=\int _{\lambda }L_{\mathrm {e} ,\Omega ,\lambda }(\lambda )\,{\overline {x}}(\lambda )\,d\lambda ,\\[6mu]Y&=\int _{\lambda }L_{\mathrm {e} ,\Omega ,\lambda }(\lambda )\,{\overline {y}}(\lambda )\,d\lambda ,\\[6mu]Z&=\int _{\lambda }L_{\mathrm {e} ,\Omega ,\lambda }(\lambda )\,{\overline {z}}(\lambda )\,d\lambda .\end{aligned}}}
ここで、
λ
{\displaystyle \lambda }
ナノメートル )である。通例的に、積分区間は
λ
∈
[
380
,
780
]
{\displaystyle \lambda \in [380,780]}
X, Y, Zの値は、分光放射輝度L e,Ω,λ で囲まれる域内に分布される。
色料の場合も色光と非常に似ているが、分光放射輝度L e,Ω,λ は色料の反射率 または透過率 S(λ) と光源の分光分布I(λ) との積に置き換えられる。
X
=
K
N
∫
λ
S
(
λ
)
I
(
λ
)
x
¯
(
λ
)
d
λ
,
Y
=
K
N
∫
λ
S
(
λ
)
I
(
λ
)
y
¯
(
λ
)
d
λ
,
Z
=
K
N
∫
λ
S
(
λ
)
I
(
λ
)
z
¯
(
λ
)
d
λ
,
{\displaystyle {\begin{aligned}X&={\frac {K}{N}}\int _{\lambda }S(\lambda )\,I(\lambda )\,{\overline {x}}(\lambda )\,d\lambda ,\\[8mu]Y&={\frac {K}{N}}\int _{\lambda }S(\lambda )\,I(\lambda )\,{\overline {y}}(\lambda )\,d\lambda ,\\[8mu]Z&={\frac {K}{N}}\int _{\lambda }S(\lambda )\,I(\lambda )\,{\overline {z}}(\lambda )\,d\lambda ,\end{aligned}}}
ここで、
N
=
∫
λ
I
(
λ
)
y
¯
(
λ
)
d
λ
,
{\displaystyle N=\int _{\lambda }I(\lambda )\,{\overline {y}}(\lambda )\,d\lambda ,}
K は換算係数であり、通常1から100の値を取る。
λ
{\displaystyle \lambda }
ナノメートル )である。 積分区間は
λ
∈
[
380
,
780
]
{\displaystyle \lambda \in [380,780]}
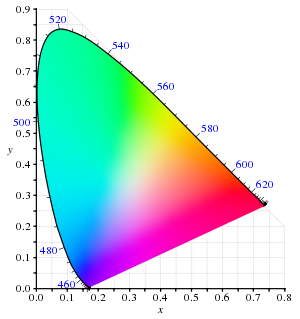
CIE 1931色空間のxy色度図。外側の曲線の境界線は、スペクトル軌跡(単色光軌跡)であり、波長(単位ナノメートル)が併記されている。 この画像にはsRGB が指定されているため、画面上sRGBの色域 外の色は正しく表示されない。この画像を表示しているディスプレイの色空間およびキャリブレーション状況により、sRGBの色そのものが正しく表示出来ないこともある。この画像は、コンピュータモニター やテレビ において彩度を最大化させて表示出来るよう作られている。 CIE 1931色空間のxy色度図。上の図と異なり、印刷等で用いられる顔料 などを用いて表現される、彩度が低い場合の色度図。併記される色の名前は マンセル表色系 の色。 ヒトの目には、三種類の色を感知するセンサーがあり、異なる領域の波長を感知するため、視覚可能な色をプロットしていくと三次元の図となる。一方で色の概念は、輝度と色度に分類される。例えば、白色は明るい色として定義され、灰色は白色の輝度が低い色ということが出来る。言い換えれば、白色の色度と、灰色の色度は同じであるが、輝度のみが異なる、といえる。
CIE XYZ色空間は、意図的にY成分が輝度 となるよう設計されている。色度はxおよびzで表され、三つのうちの二つの、三刺激値X, Y, Zを用いて正規化した値:
x
=
X
X
+
Y
+
Z
{\displaystyle x={\frac {X}{X+Y+Z}}}
y
=
Y
X
+
Y
+
Z
{\displaystyle y={\frac {Y}{X+Y+Z}}}
z
=
Z
X
+
Y
+
Z
=
1
−
x
−
y
{\displaystyle z={\frac {Z}{X+Y+Z}}=1-x-y}
x, yとYを用いて定義されるのがCIE xyY色空間で、これも広く用いられている。
三刺激値のうちXおよびZは、色度値xおよびy,Yから下記のように計算される:
X
=
Y
y
x
,
{\displaystyle X={\frac {Y}{y}}x,}
Z
=
Y
y
(
1
−
x
−
y
)
.
{\displaystyle Z={\frac {Y}{y}}(1-x-y).}
色度図を右に示す。 外側の曲線の境界線は、スペクトル軌跡 または単色光 軌跡
数学的には、色度図の色は射影平面 の領域と一致する。
色度図には、CIE XYZ色空間において下記の注目すべき点が挙げられる:
色度図は平均的な観察者が色覚できるすべての色度を表している。これらの色覚できる色とその領域は、ヒトの視覚における色域 と呼ばれている。色域の中のすべての色覚可能な色度は馬蹄形(あるいは舌のような形)に内包される。色域の端部のカーブをスペクトル軌跡とよび、スペクトル軌跡は単色光(各々の点は単一の波長と色相を持つ)と一致し、図中では波長(単位ナノメートル)が記載されている。色域の下端部を結ぶ直線は純紫軌跡
可視であるすべての色度は、x, y, z の正の値を用いて表現することができる(従ってX, Y, Zも正の値を取る)。
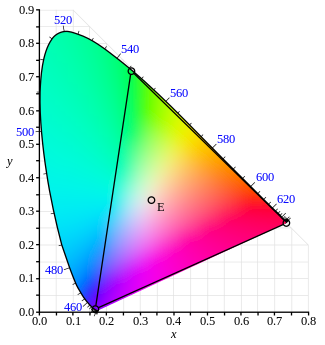
色度図において二つの任意の点を選択する。これら2点の間の直線上の色は、これら2点における二つの色の混色となる。また、色域は凸 形状となっている。色度図において、三原色を混色したすべての組み合わせの色は、三原色それぞれの点を頂点とする三角形に内包される(原色が3つ以上あるときは、その原色数の多角形内に内包される)。
二つの等しい明るさをもつ色を等量で混色させると、一般には混色させる2点間の中間点には位置しない。すなわち、CIE xy色度図では、距離が実際の色の差異とは一致しない。1940年代初頭、デビッド・マクアダム が色差と視覚感度の研究を行い、マクアダム楕円 (英語版 ) 色差 と一致すること)を目指して、CIE 1960 , CIE 1964 , CIE 1976色空間 が提案された。これらはCIE 1931色空間とは異なる手法による改善ではあったが、完全に知覚的な歪みを補正することは出来ていない。
実際に存在するの三つの光源において、ヒトの知覚できる色域を必ずしも包含出来ない場合がある。幾何学的には、3つの点からなる三角形が形成する色域は、全体の色域を内包することができない。より単純に言えば、ヒトの色域は三角形で表すことはできない。
波長(1ナノメートル間隔で等しい明るさを持つ)の尺度において、等しい明るさのスペクトルを持つ光は、(x , y ) = (1/3, 1/3) の点と一致する。
CIE RGB色空間は、RGB色空間 の一つであり、原刺激がそれぞれ単色光 である特徴を有する。
1920年代、ウィリアム・デビッド・ライトとジョン・ギルドがそれぞれ別々に行った、ヒトの色知覚に関する複数の実験結果を基にして、CIE RGB色空間とCIE XYZ色空間は定義されている。ライトの実験では、10人の被験者により行われ、ギルドの実験では7人の被験者により行われた。
CIE 1931 xy色度図上のCIE RGB色空間の色域と、3原刺激の位置。 これらの実験では、円形状のスクリーンを2分割したもの(二分視野)を用いた。また、その大きさはヒトの中心窩 よりも小さい視角である直径2度とした。片側には試験色として各単色光 が投影され、もう一方には被験者が調整可能な原色が投影される。この調整可能な原色は、等色実験では原刺激 と呼ばれる。3つの原刺激それぞれの色度 は固定されていたが、輝度 は調整できるようになっている。
被験者は、双方の色が一致するまで、3つの原刺激の輝度を調節していく。しかしながらこの方式では、試験色である各単色光の色すなわちスペクトル色 の彩度が高すぎるため、試験色を混合色と一致させることができないケースがあった。このようなケースにおいて、試験色側に原刺激のうちの1つを混色させることで、残り2つの混合色と一致させることができた。このように試験色側に原刺激を混色させる場合は、負の値の原刺激が混色されることとして扱われる。このように負の値を混色していくことで、ヒトの色覚できる範囲のすべての色を包含することが可能となった。試験色側の単色光の波長を横軸として、各々の原刺激の量をプロットすることができる。このようにして定義される、特定の実験における3つの関係式を等色関数 と呼ぶ。
CIE 1931 RGB等色関数。横軸における波長(単位:ナノメートル)の単波長光に一致させるのに必要な、各原色光の強さを表す。 ライトとギルドの等色実験では異なる種類の原刺激が用いられたが、彼らの実験結果は計算により変換され、700 nm(赤)、 546.1 nm(緑)および 435.8 nm(青)の原刺激で定義されるCIE RGB 等色関数
r
¯
(
λ
)
{\displaystyle {\overline {r}}(\lambda )}
g
¯
(
λ
)
{\displaystyle {\overline {g}}(\lambda )}
b
¯
(
λ
)
{\displaystyle {\overline {b}}(\lambda )}
r
¯
(
λ
)
{\displaystyle {\overline {r}}(\lambda )}
g
¯
(
λ
)
{\displaystyle {\overline {g}}(\lambda )}
435.8 nm でゼロ、
r
¯
(
λ
)
{\displaystyle {\overline {r}}(\lambda )}
b
¯
(
λ
)
{\displaystyle {\overline {b}}(\lambda )}
546.1 nm でゼロ、
g
¯
(
λ
)
{\displaystyle {\overline {g}}(\lambda )}
b
¯
(
λ
)
{\displaystyle {\overline {b}}(\lambda )}
700 nm でゼロとなる。これらの波長は原刺激の1つと同じためである。原刺激 546.1 nm と 435.8 nm は、水銀蒸気の放電現象により容易に再現させることができたため、選択された。700 nm の原刺激は、1931年時点では容易に再現させることは難しかったが、ヒトの目の色覚において差異を殆ど知覚できず、波長の少しの差異が全体に及ぼす影響が少ないため、選択された。
この等色関数および原刺激は、審議を経てCIEの特別委員会により承認された[ 11]
∫
0
∞
r
¯
(
λ
)
d
λ
=
∫
0
∞
g
¯
(
λ
)
d
λ
=
∫
0
∞
b
¯
(
λ
)
d
λ
.
{\displaystyle \int _{0}^{\infty }{\overline {r}}(\lambda )\,d\lambda =\int _{0}^{\infty }{\overline {g}}(\lambda )\,d\lambda =\int _{0}^{\infty }{\overline {b}}(\lambda )\,d\lambda .}
この標準化された等色関数の原刺激は、光源の輝度においてr:g:bの比が1:4.5907:0.0601、放射輝度において72.0962:1.3791:1となる。CIEはこのように原刺激の種類と単位を定義し、国際的に利用される客観的な色表記の体系を確立した。
このような数値化された等色関数により、ある色のRGBの三刺激値は、スペクトル分布
S
(
λ
)
{\displaystyle S(\lambda )}
R
=
∫
0
∞
S
(
λ
)
r
¯
(
λ
)
d
λ
,
{\displaystyle R=\int _{0}^{\infty }S(\lambda )\,{\overline {r}}(\lambda )\,d\lambda ,}
G
=
∫
0
∞
S
(
λ
)
g
¯
(
λ
)
d
λ
,
{\displaystyle G=\int _{0}^{\infty }S(\lambda )\,{\overline {g}}(\lambda )\,d\lambda ,}
B
=
∫
0
∞
S
(
λ
)
b
¯
(
λ
)
d
λ
.
{\displaystyle B=\int _{0}^{\infty }S(\lambda )\,{\overline {b}}(\lambda )\,d\lambda .}
これらはすべて内積であり、無限の次元のスペクトルを三次元色 に投影していると考えることが出来る。
ではなぜライトとギルドの実験結果が、異なる意図に基づく異なる原色光においても成立するのか?また、試験色が単波長光と一致しない場合はどうなる?という疑問が生じる。これら疑問への回答は、ヒトの色覚の線形性(近似的にほぼ線形性)に関係している。この線形性を表すのがグラスマンの法則 である。
CIE RGB色空間は通常、色度を表すのに利用される。ここで色度座標におけるr , g および b は:
r
=
R
R
+
G
+
B
,
g
=
G
R
+
G
+
B
,
b
=
B
R
+
G
+
B
.
{\displaystyle {\begin{aligned}r&={\frac {R}{R+G+B}},\\[5mu]g&={\frac {G}{R+G+B}},\\[5mu]b&={\frac {B}{R+G+B}}.\end{aligned}}}
sRGB色空間 の色域(
左 )およびD65光源下における可視光の色域(
右 )をCIE XYZ色空間上にプロットした図。
X と
Z は水平方向軸であり、
Y は垂直方向軸。
sRGB色空間 の色域(
左 )およびD65光源下における可視光の色域(
右 )をCIExyY色空間上にプロットした図。
x と
y は水平方向軸であり、
Y は垂直方向軸。
CIE RGB等色関数を使ったヒトの視覚のRGBモデルの確立の過程で、CIE特別委員会のメンバーはCIE RGB色空間と関連しつつも異なる別の色空間を定義しようと考えた。その色空間はグラスマンの法則を踏襲しつつ、CIE RGB色空間を線形変換することが検討された。この新たな色空間は、上記記載の3つの新たな等色関数
x
¯
(
λ
)
{\displaystyle {\overline {x}}(\lambda )}
y
¯
(
λ
)
{\displaystyle {\overline {y}}(\lambda )}
z
¯
(
λ
)
{\displaystyle {\overline {z}}(\lambda )}
CIE rg 色度図上で、CIE XYZ色空間を定義する三角形。Cb -Cg -Cr からなる三角形は、CIE xy 色度図においては xy = (0, 0), (0, 1), (1, 0)b と Cr を結ぶ直線は無輝面である。スペクトル軌跡は、435.8 nm におけるrg = (0, 0)546.1 nm におけるrg = (0, 1)700 nm におけるrg = (1, 0)rg = xy = (1/3, 1/3) 新たな等色関数はすべての点で負の値を取らない。1931年当時においては、手計算あるいは計算尺が使われていたため、計算を簡略化するためには正の値が望まれる。
等色関数における
y
¯
(
λ
)
{\displaystyle {\overline {y}}(\lambda )}
分光視感効率
V
(
λ
)
{\displaystyle V(\lambda )}
[ 12]
すべての光の強さが等しい白色点 では、 x = y = z = 1/3
色度とx および y が正の値をとることにより、色域内のすべての色が三角形[1, 0], [0, 0], [0, 1]に内包される。実際に色域はこの三角形の領域に完全に内包される。
等色関数における
z
¯
(
λ
)
{\displaystyle {\overline {z}}(\lambda )}
650 nm 以上においてゼロに設定でき、その精度は実験誤差の範囲にとどまる。これは計算簡略化のための必要条件である。 幾何学的観点においては、この新たな色空間を定義することは、rg 色度座標上に新たな三角形の領域を定義することと等価である。右上の図で、rg 色度座標はCIE 1931測色標準観察者の色域にそった2つの黒線の軸で描かれている。赤色の線はCIE xy 色度軸であり、上記必要条件を満たすように決められた。上記必要条件のXYZ座標値が負の値を取らないという条件については、Cr , Cg , Cb が標準観察者の色域すべてを包含することと等価である。Cr と Cb を結ぶ直線は、
y
¯
(
λ
)
{\displaystyle {\overline {y}}(\lambda )}
z
¯
(
λ
)
{\displaystyle {\overline {z}}(\lambda )}
650 nm 以上においてゼロであるという条件の意味は、Cg と Cr を結ぶ直線が、 色域内のKr の領域と接していることを表す。これは Cr の位置を表す。すべての光の強さが等しい点で x = y = 1/3b とCg の交差する点を制限する。最後に、条件の一つである色域が三角形領域に内包されるについては、緑色の領域の色域に近接するCg と Cb を結ぶ直線に第二の制限を与える。
これらの変換は、CIE RGB色空間からXYZ色空間への線形変換として定義できる。こうしてCIE特別委員会で定義された変換式は下記である:
変換行列内の数値および小数点の数については、CIE の標準が定義する数値そのものである。[ 11]
[
X
Y
Z
]
=
1
b
21
[
b
11
b
12
b
13
b
21
b
22
b
23
b
31
b
32
b
33
]
[
R
G
B
]
=
1
0.176
97
[
0.490
00
0.310
00
0.200
00
0.176
97
0.812
40
0.010
630
0.000
0
0.010
000
0.990
00
]
[
R
G
B
]
{\displaystyle {\begin{bmatrix}X\\Y\\Z\end{bmatrix}}={\frac {1}{b_{21}}}{\begin{bmatrix}b_{11}&b_{12}&b_{13}\\b_{21}&b_{22}&b_{23}\\b_{31}&b_{32}&b_{33}\end{bmatrix}}{\begin{bmatrix}R\\G\\B\end{bmatrix}}={\frac {1}{0.176\,97}}{\begin{bmatrix}0.490\,00&0.310\,00&0.200\,00\\0.176\,97&0.812\,40&0.010\,630\\0.000\,0&0.010\,000&0.990\,00\end{bmatrix}}{\begin{bmatrix}R\\G\\B\end{bmatrix}}}
上記行列の逆行列はCIEでは定義されていないものの、以下のように近似できる:
[
R
G
B
]
=
[
0.418
47
−
0.158
66
−
0.082
835
−
0.091
169
0.252
43
0.015
708
0.000
920
90
−
0.002
549
8
0.178
60
]
[
X
Y
Z
]
{\displaystyle {\begin{bmatrix}R\\G\\B\end{bmatrix}}={\begin{bmatrix}0.418\,47&-0.158\,66&-0.082\,835\\-0.091\,169&0.252\,43&0.015\,708\\0.000\,920\,90&-0.002\,549\,8&0.178\,60\end{bmatrix}}{\begin{bmatrix}X\\Y\\Z\end{bmatrix}}}
上記条件3から、XYZ等色関数の積分値はすべて等しくなり、条件2の分光視感効率の積分値からこれらの値が設定される。このため感応曲線はある程度の恣意的な値が見込まれる。X, Y, Zの感応曲線の形状は十分な精度で測定することができる。しかしながら、被験者は2つの光源が、仮に全く異なる色度であっても等しい明るさを持つかを判断しなければならないため、全体の明度曲線(実際にはこれら3曲線により重みづけの影響をうける)は主観的データである。同じ直線上において、X, Y, Zの曲線の相対的大きさは恣意的に選択されたデータである。さらには、Xの感応曲線は2倍の強さをもつものでさえ、有効な色空間として定義できてしまう。この新たな色空間は、異なる形状をもつことになる。このCIE 1931および1964 XYZ色空間の感応曲線は、これら感応曲線により同じ領域に線形写像することができる。
XYZ等色関数の比較。CIE 1931 と Stockman & Sharpe 2006 (CIE 170-2). 他のいくつかのXYZ形式の等色関数が利用可能で、元の1931色空間の既知の問題を修正している。これらの関数は、独自のXYZ形式およびxyY形式の色空間を表す。
2度視野等色関数のジャッド・フォス修正
CIEが1924年に定めた2度視野明所視標準分光視感効率
V
(
λ
)
{\displaystyle V(\lambda )}
CIE 1964 X10 Y10 Z10
X10 Y10 Z10 は、CIE 1964度視野観察者の等色関数を使用して定義されたXYZ形式の色空間である。この等色関数は、主にスタイルズとバーチのRGB等色関数から派生している。これは直接比較法で求められ、1931年の等色関数から改善されている。
スタイルズとバーチは、2度視野等色関数のセットも公開した。しかし、それらから導かれるXYZ空間はCIEによって公式に認められていない。
1931XYZ色空間のYとは異なり、Y10 は測光量には対応していない[ 13] CIE 170-2 XF YF ZF
XF YF ZF は、Stockman & Sharpe (2000) の生理学的2度視野観察者を使用して定義された XYZ形式の色空間であり、これはLMS錐体応答関数の線形結合である。等色関数のデータは、生理学的10度データセットとともに、ユニヴァーシティ・カレッジ・ロンドン のカラー&ビジョン研究所から0.1nmの解像度で入手可能である。 CIE 170-2 XF,10 YF,10 ZF,10
この空間は、Stockman & Sharpe (2000) の生理学的10度視野観察者に基づいている。
コニカミノルタ によると、古いCIE 1931 等色関数は、有機LED のような狭帯域エミッターを含む広色域ディスプレイで条件等色の不成立色が同じように見えるタイミングを予測できない)を示すが、2015 XF,10 YF,10 ZF,10 等色関数は影響を受けない。古いソニー のマニュアルでは、使用するディスプレイ技術に応じて白色点 にオフセットを適用するジャッド・フォス修正の使用を推奨している。
^ CIE (1932). Commission internationale de l'Eclairage proceedings, 1931 . Cambridge: Cambridge University Press ^ Smith, Thomas; Guild, John (1931–32). “The C.I.E. colorimetric standards and their use”. Transactions of the Optical Society 33 (3): 73–134. doi :10.1088/1475-4878/33/3/301 . ^ Wright, William David (1928). “A re-determination of the trichromatic coefficients of the spectral colors”. Transactions of the Optical Society 30 (4): 141–164. doi :10.1088/1475-4878/30/4/301 . ^ Guild, J. (1932). “The colorimetric properties of the spectrum”. Philosophical Transactions of the Royal Society of London. Series A, Containing Papers of a Mathematical or Physical Character 230 : 149–187. doi :10.1098/rsta.1932.0005 . JSTOR 91229 . ^ 篠田博之・藤枝 一郎『色彩工学入門 定量的な色の理解と活用』森北出版株式会社、2007年、42-43頁。ISBN 9784627846814 。 ^ [1] Tristimulus Value of Color : Device Independent Color Representation^ Stiles, W. S.; Birch, J. M. (1959). “N.P.L. Colour-matching Investigation: Final Report (1958)”. Optica Acta 6 (1): 1–26. doi :10.1080/713826267 . ^ Speranskaya, N. I. (1959). “Determination of spectrum color co-ordinates for twenty seven normal observers”. Optics and Spectroscopy 7 : 424–428. ^ Harris, A. C.; Weatherall, I. L. (September 1990). “Objective evaluation of color variation in the sand-burrowing beetle Chaerodes trachyscelides White (Coleoptera: Tenebrionidae ) by instrumental determination of CIE LAB values” . Journal of the Royal Society of New Zealand (The Royal Society of New Zealand) 20 (3): 253–259. doi :10.1080/03036758.1990.10416819 . オリジナル の2017-03-08時点におけるアーカイブ。. https://web.archive.org/web/20170308150820/https://books.google.com/books?id=ErI4AAAAIAAJ&pg=PA254&dq=cie+standard-observer . ^ a b Wyman, Chris; Sloan, Peter-Pike; Shirley, Peter (July 12, 2013). “Simple Analytic Approximations to the CIE XYZ Color Matching Functions” . Journal of Computer Graphics Techniques 2 (2): 1-11. ISSN 2331-7418 . http://jcgt.org/published/0002/02/01/ .
^ a b Fairman, H. S. (February 1997). “How the CIE 1931 Color-Matching Functions Were Derived from the Wright–Guild Data”. Color Research and Application 22 (1): 11–23. doi :10.1002/(SICI)1520-6378(199702)22:1<11::AID-COL4>3.0.CO;2-7 .
^ CIE (1926). Commission internationale de l'éclairage proceedings, 1924 . Cambridge: Cambridge University Press 460 nm , and has been supplemented with newer and more accurate luminosity curves; see Luminosity function#Improvements to the standard .^ 大田登『色彩工学 第2版』東京電機大学出版局、2001年、108頁。ISBN 4501618906 。
色彩科学
基礎的概念 色の三属性 色名
分野
研究者 表色系(色空間)
色彩の組織 関連項目







![{\displaystyle {\begin{bmatrix}X\\Y\\Z\end{bmatrix}}=\left[{\begin{aligned}1&.910\,20\!\!\!&\!\!-1&.112\,12\!\!\!&\!\!0&.201\,91\\0&.370\,95\!\!\!&\!\!0&.629\,05\!\!\!&\!\!0&\\0&\!\!\!&\!\!0&\!\!\!&\!\!1&.000\,00\end{aligned}}\right]{\begin{bmatrix}L\\M\\S\end{bmatrix}}_{\rm {HPE}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4a15573a77cd48decc68aada921e4ff01a6d24e2)






![{\displaystyle g(x;\mu ,\sigma _{1},\sigma _{2})={\begin{cases}\exp {\bigl (}{-{\tfrac {1}{2}}(x-\mu )^{2}/\sigma _{1}^{2}}{\bigr )},&x<\mu ,\\[2mu]\exp {\bigl (}{-{\tfrac {1}{2}}(x-\mu )^{2}/\sigma _{2}^{2}}{\bigr )},&x\geq \mu .\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0479d8adc9d0750a8a313ebd91e84cda67fd3074)
![{\displaystyle {\begin{aligned}{\overline {x}}(\lambda )&=1.056g(\lambda ;599.8,37.9,31.0)+0.362g(\lambda ;442.0,16.0,26.7)\\[2mu]&\quad -0.065g(\lambda ;501.1,20.4,26.2),\\[5mu]{\overline {y}}(\lambda )&=0.821g(\lambda ;568.8,46.9,40.5)+0.286g(\lambda ;530.9,16.3,31.1),\\[5mu]{\overline {z}}(\lambda )&=1.217g(\lambda ;437.0,11.8,36.0)+0.681g(\lambda ;459.0,26.0,13.8).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8f49afe796c9961188fc3a14d1b5de9bbcf359a6)
![{\displaystyle {\begin{aligned}X&=\int _{\lambda }L_{\mathrm {e} ,\Omega ,\lambda }(\lambda )\,{\overline {x}}(\lambda )\,d\lambda ,\\[6mu]Y&=\int _{\lambda }L_{\mathrm {e} ,\Omega ,\lambda }(\lambda )\,{\overline {y}}(\lambda )\,d\lambda ,\\[6mu]Z&=\int _{\lambda }L_{\mathrm {e} ,\Omega ,\lambda }(\lambda )\,{\overline {z}}(\lambda )\,d\lambda .\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f62d8f94207fbbf4909ab58734898c6fcae324d5)

![{\displaystyle \lambda \in [380,780]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4a2085e55423178ed3ce092367c2038d1af45d83)
![{\displaystyle {\begin{aligned}X&={\frac {K}{N}}\int _{\lambda }S(\lambda )\,I(\lambda )\,{\overline {x}}(\lambda )\,d\lambda ,\\[8mu]Y&={\frac {K}{N}}\int _{\lambda }S(\lambda )\,I(\lambda )\,{\overline {y}}(\lambda )\,d\lambda ,\\[8mu]Z&={\frac {K}{N}}\int _{\lambda }S(\lambda )\,I(\lambda )\,{\overline {z}}(\lambda )\,d\lambda ,\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c448fc8038f4d343e3efefd50cdeba2154a14f59)











![{\displaystyle {\begin{aligned}r&={\frac {R}{R+G+B}},\\[5mu]g&={\frac {G}{R+G+B}},\\[5mu]b&={\frac {B}{R+G+B}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/15cfc20b09a52c5f725cead93f5671c6564ed4a5)



