Energia de Fermi
|
Read other articles:

Questa voce sull'argomento montagne del Canada è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Montagne Rocciose CanadesiPosizione delle Montagne Rocciose CanadesiContinenteAmerica settentrionale Stati Canada Catena principaleMontagne Rocciose Cima più elevataMonte Robson (3.954 m s.l.m.) Il Ringrose Peak e il lago O'Hara, British Columbia, Canada Le Montagne Rocciose Canadesi, come dice il loro nome, costituiscono il segmento canadese del…

Bagian dari seriIslam Rukun Iman Keesaan Allah Malaikat Kitab-kitab Allah Nabi dan Rasul Allah Hari Kiamat Qada dan Qadar Rukun Islam Syahadat Salat Zakat Puasa Haji Sumber hukum Islam al-Qur'an Sunnah (Hadis, Sirah) Tafsir Akidah Fikih Syariat Sejarah Garis waktu Muhammad Ahlulbait Sahabat Nabi Khulafaur Rasyidin Khalifah Imamah Ilmu pengetahuan Islam abad pertengahan Penyebaran Islam Penerus Muhammad Budaya dan masyarakat Akademik Akhlak Anak-anak Dakwah Demografi Ekonomi Feminisme Filsafat Ha…

Didit HediprasetyoLahir22 Maret 1984 (umur 40)Jakarta, IndonesiaTempat tinggalParis, PrancisKebangsaanIndonesiaAlmamaterParsons School of DesignÉcole Parsons à ParisPekerjaanPerancang busanaOrang tuaPrabowo Subianto (bapak)Titiek Soeharto (ibu)Situs webdidithediprasetyo.com Ragowo Hediprasetyo Djojohadikusumo atau Didit Hediprasetyo (lahir 22 Maret 1984) adalah seorang perancang busana Indonesia yang berprestasi di kancah internasional. Ia merupakan putra tunggal dari Prabowo Subianto dan…

Josh Hawley Senator Amerika Serikat dari MissouriPetahanaMulai menjabat 3 Januari 2019Menjabat bersama Roy Blunt PendahuluClaire McCaskillPenggantiPetahanaJaksa Agung Missouri ke-42Masa jabatan9 Januari 2017 – 3 Januari 2019GubernurEric GreitensMike Parson PendahuluChris KosterPenggantiEric Schmitt Informasi pribadiLahirJoshua David Hawley31 Desember 1979 (umur 44)Springdale, Arkansas, Amerika SerikatPartai politikRepublikSuami/istriErin Morrow (m. …

43rd season of the UEFA club football tournament 1997–98 UEFA Champions LeagueThe Amsterdam Arena held the finalTournament detailsDatesQualifying:23 July – 27 August 1997Competition proper:17 September 1997 – 20 May 1998TeamsCompetition proper: 24Total: 55Final positionsChampions Real Madrid (7th title)Runners-up JuventusTournament statisticsMatches played85Goals scored239 (2.81 per match)Attendance2,868,568 (33,748 per match)Top scorer(s)Alessandro Del Piero (Juventus)10 go…

Estonian football club Football clubFC Nõmme UnitedFull nameJalgpalliklubi FC Nõmme UnitedFounded2000; 24 years ago (2000)GroundMänniku StadiumCapacity500PresidentMart PoomManagerJani SarajärviLeagueMeistriliiga2023Esiliiga, 1st of 10 (promoted)WebsiteClub website Home colours Away colours FC Nõmme United is an Estonian professional football club based in Nõmme, a district in Tallinn. The club was founded in 2000 and from the 2024 season competes in the Meistriliiga, the …

Kapisa کاپیساProvinsiLokasi di AfganistanNegaraAfghanistanIbu kotaMahmud-i-RaqiLuas • Total1.842,1 km2 (7,112 sq mi)Populasi (2015)[1] • Total441.010 • Kepadatan24/km2 (62/sq mi)Zona waktuUTC+4:30Kode ISO 3166AF-KAPBahasa utamaPashtun, Dari, Pashayi Kapisa (Pashtun/Persia: کاپيسا) adalah salah satu dari tiga puluh empat provinsi di Afganistan. Provinsi ini terletak di timur laut negeri itu dan beribu kota di Mahmud-…

Untuk kitab Alkitab, lihat Kitab Maleakhi. Maleakhi, dalam sebuah lukisan karya Duccio di Buoninsegna, c. 1310 (Museo dell'Opera del Duomo, Katedral Siena). Maleakhi atau Mal'akhi (מַלְאָכִי Utusan/malaikatku, Ibrani Standar Malʾaḫi, Ibrani Tiberias Malʾāḵî) adalah seorang nabi dalam Alkitab Ibrani (atau Tanakh bagi umat Yahudi) dan Perjanjian Lama di Alkitab umat Kristen. Maleakhi adalah nabi terakhir dalam urutan nabi-nabi kecil, dan penulis Kitab Maleakhi, kitab terakhir dala…

Voce principale: National Basketball Association 1953-1954. NBA Playoffs 1954Il logo delle FinaliDettagli della competizioneSport Pallacanestro OrganizzatoreNBA Periodo16 marzo 1954 —12 aprile 1954 Data1954 Squadre6 VerdettiTitolo East Syracuse Nationals Titolo West Minneapolis Lakers Campione Minneapolis Lakers(5º titolo) Cronologia della competizioneed. successiva → ← ed. precedente Modifica dati su Wikidata · Manuale Gli NBA Playoffs…
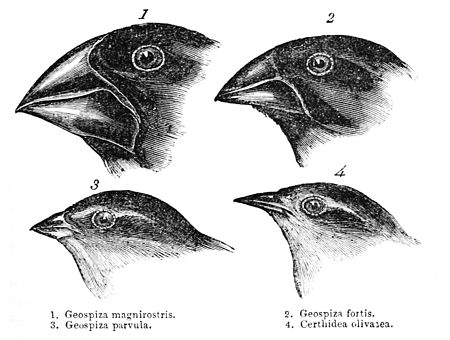
Study of changes in physiological characteristics Natural and sexual selection are often presumed to act most directly on behavior (e.g., what an animal chooses to do when confronted by a predator), which is expressed within limits set by whole-organism performance abilities (e.g., how fast it can run) that are determined by subordinate traits (e.g., muscle fiber-type composition). A weakness of this conceptual and operational model is the absence of an explicit recognition of the place of life …

AwardMedal for Long Service, BronzeTypeMilitary long service medalAwarded forTen years faithful serviceCountry CiskeiPresented bythe PresidentEligibilityAll RanksStatusDiscontinued in 1994Established1988Ribbon bar CDF pre-1994 & SANDF post-2002 orders of wearNext (higher)CDF precedence: Independence Medal SANDF precedence: Faithful Service Medal Next (lower)CDF succession: President's Medal for Shooting SANDF succession: Bronze Service Medal The Medal for Long Service, Bronze was i…

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Gunung Batubrok – berita · surat kabar · buku · cendekiawan · JSTOR Gunung BatubrokTitik tertinggiKetinggian1.546 m (5.072 kaki)GeografiLetakKalimantan , IndonesiaPegununganMuller SchwanerGeologiJ…

Hartarto Sastrosoenarto Menteri Negara Koordinator Pendayagunaan Aparatur Negara Indonesia ke-7Masa jabatan16 Maret 1998 – 20 Oktober 1999PresidenSoehartoB. J. HabibiePendahuluT.B. SilalahiPenggantiFreddy NumberiMenteri Negara Koordinator Bidang Perekonomian Indonesiaad-interimMasa jabatan1 Oktober 1999 – 20 Oktober 1999PresidenB. J. HabibiePendahuluGinandjar KartasasmitaPenggantiKwik Kian GieMenteri Koordinator Bidang Produksi dan Distribusi Indonesia ke-3Masa jaba…

Confederate Army general (1814–1875) For the American sugar industry executive, see Henry Arthur Benning. Henry L. BenningPortrait of Gen. Henry Lewis Benning by Bjorn EgeliBirth nameHenry Lewis BenningNickname(s)Old RockBorn(1814-04-02)April 2, 1814Columbia County, Georgia, U.S.DiedJuly 10, 1875(1875-07-10) (aged 61)Columbus, Georgia, U.S.BuriedLinwood CemeteryColumbus, Georgia, U.S.AllegianceConfederate States of AmericaService/branchConfederate States ArmyYears of service1861–18…

Canadian founded by the Weeknd XOParent companyUniversal Music GroupFounded2011; 13 years ago (2011)Founder The Weeknd Wassim Slaiby Amir Esmailian La Mar Taylor StatusActiveDistributor(s)Republic RecordsGenreR&Bhip hopCountry of originCanada XO (also known as XO)[1][2] is a Canadian record label founded by singer the Weeknd, his managers Wassim Slaiby and Amir Cash Esmailian, and his creative director La Mar Taylor.[3] Slaiby also serves as the CEO.…

「俄亥俄」重定向至此。关于其他用法,请见「俄亥俄 (消歧义)」。 俄亥俄州 美國联邦州State of Ohio 州旗州徽綽號:七葉果之州地图中高亮部分为俄亥俄州坐标:38°27'N-41°58'N, 80°32'W-84°49'W国家 美國加入聯邦1803年3月1日,在1953年8月7日追溯頒定(第17个加入联邦)首府哥倫布(及最大城市)政府 • 州长(英语:List of Governors of {{{Name}}}]]) • …

Zikhron TuvyaLingkunganNegara IsraelProvinsiYerusalemKotaYerusalemZona waktuUTC+3 (EAT) • Musim panas (DST)UTC+3 (EAT) Zikhron Tuvya adalah sebuah lingkungan di kota suci Yerusalem di Provinsi Yerusalem, tepatnya di sebelah timur Israel.[1] Referensi ^ National Geospatial-Intelligence Agency. GeoNames database entry. (search Diarsipkan 2019-09-08 di Wayback Machine.) Accessed 12 May 2011. lbsLingkungan di YerusalemLingkungan-lingkungan Yerusalem sebelah timur garis genca…

Wakil Gubernur BantenLambang provinsiPetahanalowongsejak 12 Mei 2022Masa jabatan5 tahunPejabat perdanaRatu Atut ChosiyahDibentuk11 Januari 2002; 22 tahun lalu (2002-01-11)Situs webSitus web resmi Wakil Gubernur Banten merupakan wakil kepala daerah di Banten yang bertugas menjalankan pemerintahan dan membuat kebijakan-kebijakan daerah, seperti membuat peraturan daerah bersama dengan DPRD Provinsi Banten, dan sebagainya. Dalam mengemban tugas-tugas tertentu, seorang wakil gubernur mendam…

St. Burchard's AbbeyKloster St. Burkard, WürzburgView of the church from Marienberg FortressLocation within BavariaShow map of BavariaSt. Burchard's Abbey, Würzburg (Germany)Show map of GermanyMonastery informationOrderBenedictinesEstablishedca. 750Disestablished1803Dedicated toMary, Andrew, Magnus, BurchardDioceseDiocese of WürzburgControlled churchesSt. BurchardPeopleFounder(s)Bishop Burchard of WürzburgArchitectureStyleRomanesque/GothicSiteLocationWürzburg, GermanyCoordinates49°47′23.…
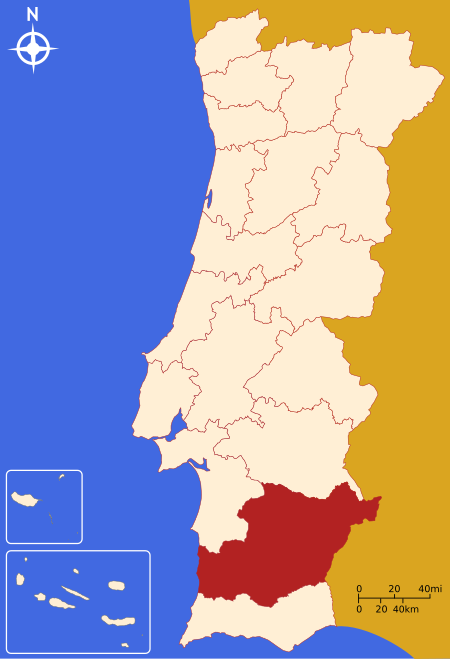
District of Portugal For other uses, see Beja (disambiguation). District in Alentejo, PortugalDistrict of BejaDistrict FlagCoat of armsCountryPortugalRegionAlentejoHistorical provinceBaixo AlentejoNo. of municipalities14No. of parishes75CapitalBejaArea • Total10,225 km2 (3,948 sq mi)Population (2011) • Total152,758 • Density15/km2 (39/sq mi)ISO 3166 codePT-02No. of parliamentary representatives3 The Beja District (Portuguese pronunciat…
![{\displaystyle \mu =\epsilon _{F}\left[1-{\frac {\pi ^{2}}{12}}\left({\frac {kT}{\epsilon _{F}}}\right)^{2}+{\frac {\pi ^{4}}{80}}\left({\frac {kT}{\epsilon _{F}}}\right)^{4}+...\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/80462a105fffc6a82aab94ce41c209b37211f333)





















![{\displaystyle E_{t}={\frac {3}{5}}N_{0}E_{f}={\frac {3}{5}}N_{0}\left[{\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}\left({\frac {3N_{0}}{\pi }}\right)^{2/3}\right]={\frac {3^{\frac {5}{3}}\pi ^{\frac {4}{3}}\hbar ^{2}}{10mL^{2}}}N_{0}^{\frac {5}{3}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ac09bbd4ff9cff66bb792332332a91f88d8d6a79)








