Вихревое движение
|
Read other articles:

The RiverSutradaraPare LorentzDitulis olehPare LorentzSinematograferFloyd CrosbyWillard Van DykeStacy WoodardDistributorFarm Security AdministrationTanggal rilis4 Februari 1938 (1938-02-04)Durasi31 menitNegaraAmerika SerikatBahasaInggris The River adalah sebuah film dokumenter pendek 1938 yang menampilkan pengaruh Sungai Mississippi bagi Amerika Serikat, dan kenapa praktik penebangan dan perkebunan telah menyebabkan pengikisan tanah di pinggiran sungai dan Teluk Meksiko, berujung pada banji…

Hotarubi no Mori e蛍火の杜へ MangaPengarangYuki MidorikawaPenerbitHakusenshaTerbit10 Juli 2003Volume1 Film animeSutradaraTakahiro OmoriStudioBrains BaseTayang2011 Portal anime dan manga Hotarubi no Mori e (蛍火の杜へcode: ja is deprecated ) adalah sebuah manga tahun 2003 ditulis oleh pengarang Yuki Midorikawa. Manga ini telah diadaptasi menjadi sebuah film pada tahun 2011.[1] Referensi ^ News: Yuki Midorikawa's Hotarubi no Mori e Manga Gets Anime Film (dalam bahasa In…

هذه مقالة غير مراجعة. ينبغي أن يزال هذا القالب بعد أن يراجعها محرر؛ إذا لزم الأمر فيجب أن توسم المقالة بقوالب الصيانة المناسبة. يمكن أيضاً تقديم طلب لمراجعة المقالة في الصفحة المخصصة لذلك. (أكتوبر 2018) هذه المقالة عن زاوية سيدي الطيب العيشوني. لمعانٍ أخرى، طالع سيدي الطي…

Strada statale 107Silana CrotoneseLocalizzazioneStato Italia Regioni Calabria Province Cosenza Crotone DatiClassificazioneStrada statale InizioInnesto con la SS 18 presso Paola FineInnesto con la SS 106 al bivio Passovecchio presso Crotone Lunghezza137,300 km Provvedimento di istituzioneLegge 17 maggio 1928, n. 1094 PercorsoStrade europee Manuale La strada statale 107 Silana Crotonese è una strada statale italiana. Indice 1 Aspetti generali 2 L'importanza strategica 3 I mari…

Town in Virginia, United StatesEdinburg, VirginiaTownThe Mill in Edinburg, Virginia (1848).Location in VirginiaCoordinates: 38°49′21″N 78°33′55″W / 38.82250°N 78.56528°W / 38.82250; -78.56528CountryUnited StatesStateVirginiaCountyShenandoahFounded1852Government • MayorDaniel J. HarshmanArea[1] • Total0.76 sq mi (1.96 km2) • Land0.74 sq mi (1.92 km2) • Water0.02 sq m…

CF-18B McDonnell Douglas CF-18 Hornet (sebutan resmi militer CF-188 ) merupakan pesawat tempur Royal Canadian Air Force (RCAF) (sebelumnya Canadian Forces Air Command), berdasarkan pesawat tempur Amerika McDonnell Douglas F/A-18 Hornet. Pada tahun 1980, F/A-18 terpilih sebagai pemenang kompetisi Pesawat Fighter Baru, dan dianugerahi pesanan produksi. Pasukan Kanada mulai menerima CF-18 pada tahun 1982. CF-18 telah mendukung kedaulatan patroli udara NORAD dan berpartisipasi dalam pertempuran sela…

Political party in Australia Nationalist Alternative Australian Nationalist AlternativeAbbreviationNatAltNAFoundedc. 2009Dissolvedc. 2019Ideology Neo-fascism[1] White nationalism[2][3] Anti-semitism[2][3] Anti-LGBT[1] Anti-immigration[2][4] Political positionFar-right[2][5][6][7]Colours Blue and WhitePolitics of AustraliaPolitical partiesElections Part of a series onFar-right pol…

Cet article est une ébauche concernant un coureur cycliste belge. Vous pouvez partager vos connaissances en l’améliorant (comment ?). Pour plus d’informations, voyez le projet cyclisme. Yves CoolenYves Coolen lors du départ du Mémorial Philippe Van Coningsloo 2015 à Wavre.InformationsNaissance 25 septembre 1995 (28 ans)TurnhoutNationalité belgeÉquipes non-UCI 2015-2016Rock Werchter-Toekomstvrienden2017-2018Home Solution-Anmapa-SoenensÉquipes UCI 2019-2020BEAT Cycling Club 2…

1911 American filmThe Fishermaid of BallydavidThe Pictures (Vol 1 n°11, December 31, 1911).Directed bySidney OlcottWritten byGene GauntierProduced byKalem CompanyStarringGene GauntierSidney OlcottCinematographyGeorge K. HollisterRelease date November 17, 1911 (1911-11-17) Running time1000 ftCountryUnited StatesLanguagesSilent film(English intertitles) The Fishermaid of Ballydavid is a 1911 American silent film produced by Kalem Company. It was directed by Sidney Olcott with himse…

Pelabuhan Wicklow Wicklow (bahasa Irlandia: Cill Mhantáin berarti Gereja Ompong) ialah ibu kota county dengan nama yang sama di Republik Irlandia. Terletak di selatan ibu kota negara Dublin di pesisir timur Pulau Irlandia, kota ini berpenduduk sekitar 9.355 jiwa. Kota ini terletak di jalan nasional N11 yang menghubungkan Dublin dengan Wexford, dan juga terhubung dengan layanan kereta api komuter dengan Dublin. Layanan tambahan menghubungkannya dengan Arklow, Wexford dan Rosslare, pelabuhan feri…

Marcia CrossLahirMarcia Anne CrossPekerjaanAktrisTahun aktif1984–sekarangSuami/istri(Almarhum) Richard Jordan (1985 - 1993)Tom Mahoney (2006 - sekarang)Anak(kembar) Eden Mahoney dan Savannah Mahoney (2007) Marcia Anne Cross (lahir 25 Maret 1962 di Marlborough, Massachusetts) merupakan seorang aktris berkebangsaan Amerika Serikat yang memenangkan Emmy dan Golden Globe Award. Dia menikah dengan Tom Mahoney sejak tahun 2006 dan saat ini memiliki 2 orang anak: putri kembar Eden dan Savannah M…

George Harrison: Living in the Material WorldSutradaraMartin ScorseseProduserOlivia HarrisonMartin ScorseseNigel SinclairPemeranGeorge HarrisonSinematograferRobert RichardsonMartin KenziePenyuntingDavid TedeschiDistributorHBOTanggal rilis 5 Oktober 2011 (2011-10-05) Durasi208 minNegaraUnited StatesBahasaEnglish George Harrison: Living in the Material World adalah film dokumenter Amerika Serikat Inggris produksi tahun 2011 yang disutradarai oleh Martin Scorsese, diangkat dari kisah nyata keh…

Questa voce sull'argomento contee dell'Illinois è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Contea di McDonoughconteaLocalizzazioneStato Stati Uniti Stato federato Illinois AmministrazioneCapoluogoMacomb Data di istituzione1826 TerritorioCoordinatedel capoluogo40°27′36″N 90°40′48″W / 40.46°N 90.68°W40.46; -90.68 (Contea di McDonough)Coordinate: 40°27′36″N 90°40′48″W / 40.46°N 90.68°W4…

Part of a series on the History of Taiwan Chronological Prehistory to 1624 Dutch Formosa 1624–1662 Spanish Formosa 1626–1642 Kingdom of Tungning 1662–1683 Qing rule 1683–1895 Republic of Formosa 1895 Japanese rule 1895–1945 Republic of China rule 1945–present Topical Cultural Economic Educational Historiography LGBT Military Television Local Kaohsiung Taipei Kingdom of Middag Lists Timeline Rulers Archaeological sites Taiwan portalvte Most information about Taiwan before th…

American stew For other uses, see Booya. BooyahAmerican-style booyah stewTypeStewPlace of originUnited StatesRegion or stateUpper MidwestMain ingredientsMeat (commonly beef, chicken, or pork), vegetables (carrots, peas, onion, celery, rutabagas potatoes), seasonings Booyah (also spelled booya, bouja, boulyaw, or bouyou) is a thick stew, believed to have originated in Belgium, and made throughout the Upper Midwestern United States.[1] Booyah can require up to two days and multiple cooks t…

Vince GillInformasi latar belakangNama lahirVincent Grant GillLahir12 April 1957 (umur 67)Norman, Oklahoma, ASGenreCountry, bluegrass, blue-eyed soul, country pop, Southern rockPekerjaanPenyanyi, Penulis LaguInstrumenVokal, gitarTahun aktif1979–sekarangLabelRCA Nashville, MCA, MCA NashvilleArtis terkaitThe Notorious Cherry Bombs, Pure Prairie League, Rodney Crowell, Ricky Skaggs, EaglesSitus webvincegill.com Vincent Grant Gill (lahir 12 April 1957) adalah seorang penyanyi, penulis lagu da…
Кинопоиск URL kinopoisk.ru Коммерческий да Тип сайта информационный сервис о киноонлайн-кинотеатр Регистрация необязательная для ознакомления,обязательная для социальных возможностей, добавления и редактирования информации, рецензий, комментариев Язык (-и) русский, английс…

German politician (1954–2017) Schurer in August 2017 Ewald Schurer (15 April 1954 – 2 December 2017) was a German politician for the Social Democratic Party (SPD). At the time of death, he had been serving in the Bundestag since 2005. He had previously served in the Bundestag from 1998 to 2002. He was elected to the local council of Ebersberg, Bavaria in 1984. A Roman Catholic, Schurer was married with four children.[1] He ran unsuccessfully in Erding – Ebersberg in 2009, 2013 and …
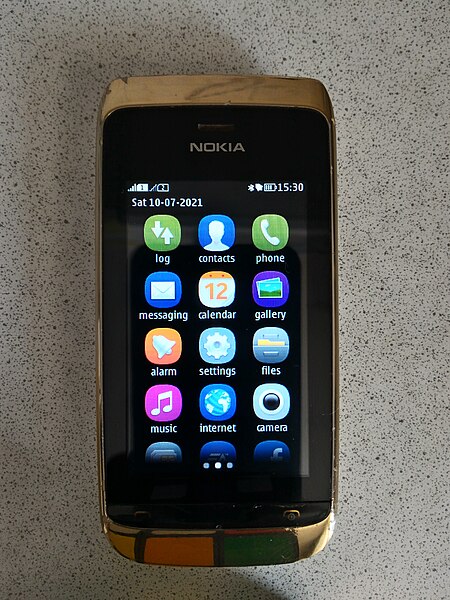
نوكيا آشا 308معلومات عامةالنوع هاتف محمول الصانع نوكياعائلة المنتج لمس مكتملالألوان ذهبي[1] — أسود[1] موقع الويب nokia.com… (لغات متعددة) أهم التواريختاريخ الإصدار آكتوبر 2012الوظائفالشاشة شاشة لمس 240 × 400الكاميرا - الخلفية:2 ميجابكسلالإدخال شاشة لمس متعددالخصائصالذاكرة 64 �…

English gothic rock band This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: The Mission band – news · newspapers · books · scholar · JSTOR (June 2021) (Learn how and when to remove this message) The MissionThe Mission performing in 2017Background informationOriginLeeds, EnglandGenresGothic rockpost-punkhard r…












