Среднее арифметическое
|
Read other articles:

Manuel Sondakh Sekretaris Jenderal Partai Kristen IndonesiaMasa jabatan5 Februari 1961 – 11 Februari 1962PresidenSoekarno PendahuluHandrianus SinagaPenggantiChristian MooyAnggota Dewan Perwakilan RakyatMasa jabatan24 Maret 1956 – 26 Juni 1960PresidenSoekarnoAnggota Dewan Perwakilan Rakyat Gotong RoyongMasa jabatan26 Juni 1960 – 15 November 1965PresidenSoekarno Informasi pribadiLahir(1905-12-25)25 Desember 1905 Motoling, Manado, Hindia BelandaMeninggal18 November …

French explorer Binot Paulmier de Gonneville. Binot Paulmier, sieur de Gonneville, French navigator of the early 16th century, was widely believed in 17th and 18th century France to have been the discoverer of the Terra Australis.[1] Currently, history books from Normandy, in France, teach that Binot Paulmier was a French-Norman navigator who arrived in what is now Southern Brazil in 1504.[2][3][4] According to his published memories, in 1503 de Gonneville, challe…

Chikita FawziLahirMarsha Chikita Fawzi28 Januari 1989 (umur 35)Jakarta, IndonesiaNama lainChikita FawziAlmamaterMultimedia University SelangorPekerjaanAktrisaktivisanimatorpenyanyiTahun aktif2010–sekarang Marsha Chikita Fawzi (lahir 28 Januari 1989) adalah seorang aktivis, animator, pemeran dan penyanyi Indonesia. Bungsu dari keluarga Fawzi, ia merupakan adik dari pemeran dan penyiar televisi Indonesia, Isabella Fawzi. Karier Sebagai animator Sejak pertengahan 2000-an, Chiki men…

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Maret 2016. SMA Negeri 1 WonotunggalInformasiDidirikan8 Mei 2007AkreditasiBNomor Pokok Sekolah Nasional20337813MaskotBlue GaneshaKepala SekolahMuch. Kuntoaji, S.Pd,.M.Pd.B.IJurusan atau peminatanIPA, dan IPSRentang kelasX, XI IPA, XI IPS, XII IPA, XII IPS,Kurikulu…

Jabalpur merupakan sebuah kota di India. Kota ini letaknya di bagian tengah. Tepatnya di negara bagian Madhya Pradesh di distrik Jabalpur. Pada tahun 2001, kota ini memiliki jumlah penduduk 1.117.200 jiwa dan memiliki luas wilayah 10.000 km². Kota ini memiliki angka kepadatan penduduk 110 jiwa/km². JabalpurMetropolisDari atas: Kuil Shiva city kachnar, Pengadilan Tinggi MP, Jabalpur Engineering College & Air Terjun DhuandharJulukan: Sanskaar Dhaani, Tripur TirthJabalpurLocation of…

Questa voce o sezione sull'argomento calcio non è ancora formattata secondo gli standard. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Voce principale: Nazionale di calcio dell'Italia. Italia Universitaria Uniformi di gara Casa Trasferta Sport Calcio Federazione FIGC Soprannome Azzurri Selezionatore Carica vacante Esordio internazionale Italia 3-2 Austria 17 luglio 1927 Migliore vittoria Italia 10-0 Svizzera 29 agosto 192…

View from Point Judith ferry dock Galilee is a fishing village on Point Judith within the town of Narragansett, Rhode Island, USA, and is notable for being home to the largest fishing fleet in Rhode Island and for being the site of the Block Island Ferry. The village is directly across the harbor from Jerusalem, Rhode Island. Galilee, Rhode Island is named after the Biblical Galilee, which was the original home region of Jesus Christ, who grew up in Nazareth, a village in the Galilee region of I…

VBMR Griffon VBMR Griffon pada pameran Jenis Pengangkut personel lapis baja Negara asal Prancis Sejarah pemakaian Masa penggunaan 2018 - sekarang Digunakan oleh Prancis, Belgia Sejarah produksi Produsen Nexter, Thales, Arquus Biaya produksi €1 juta/kendaraan Diproduksi 2018 - sekarang Varian APC / Pos komando / Ambulans / Pelihat artileri Spesifikasi Berat 24,5 ton Lebar 25 m (82 ft 0 in) Tinggi 30 m (98 ft 5 in) Awak 2 (pengemudi+penembak) Sen…

2013 studio album by Tedeschi Trucks BandMade Up MindStudio album by Tedeschi Trucks BandReleasedAugust 20, 2013 (2013-08-20)StudioSwamp Raga Studios (Jacksonville, Florida)Genre Rock R&B soul Length53:14LabelMasterworksProducer Jim Scott Derek Trucks Tedeschi Trucks Band chronology Everybody's Talkin'(2012) Made Up Mind(2013) Let Me Get By(2016) Professional ratingsAggregate scoresSourceRatingMetacritic76/100[1]Review scoresSourceRatingAmerican Songwriter[…

Artikel ini membutuhkan rujukan tambahan agar kualitasnya dapat dipastikan. Mohon bantu kami mengembangkan artikel ini dengan cara menambahkan rujukan ke sumber tepercaya. Pernyataan tak bersumber bisa saja dipertentangkan dan dihapus.Cari sumber: Emetofilia – berita · surat kabar · buku · cendekiawan · JSTOR Orang yang sedang muntah Emetophilia adalah gairah seksual saat muntah, atau melihat orang lain muntah.[1] Kadang-kadang disebut sebagai fet…

Piala Negara-Negara Afrika 1994كأس أمم إفريقيا 1994 (Bahasa Arab) Coupe d'Afrique des Nations 1994 (Bahasa Prancis)Informasi turnamenTuan rumah TunisiaJadwalpenyelenggaraan26 Maret s.d. 10 April 1994Jumlahtim peserta12 (dari 1 konfederasi)Tempatpenyelenggaraan3 (di 2 kota)Hasil turnamenJuara Nigeria (gelar ke-2)Tempat kedua ZambiaTempat ketiga Pantai GadingTempat keempat MaliStatistik turnamenJumlahpertandingan20Jumlah gol44 (2,2 per pertandin…

لمعانٍ أخرى، طالع عاصمة الثقافة (توضيح). هذه المقالة بحاجة لصندوق معلومات. فضلًا ساعد في تحسين هذه المقالة بإضافة صندوق معلومات مخصص إليها. شعار مدينة ليفربول كعاصمة للثقافة الأوروبية يرفف على أحد الأعلام عواصم الثقافة الأوروبية، هي إحدى المبادرات الثقافية التي قام ب…

Spanish sports TV channel Television channel GOL PLAYCountrySpainBroadcast areaSpain, AndorraHeadquartersBarcelona, SpainProgrammingLanguage(s)SpanishPicture format1080i HDTVOwnershipOwnerMediaproHistoryLaunched19 September 2008; 15 years ago (2008-09-19) (as pay channel)1 June 2016; 7 years ago (2016-06-01) (as free-to-air channel)ReplacedHogar 10Closed30 June 2015; 8 years ago (2015-06-30) (as pay channel)Replaced bybeIN Sports (for pay cha…
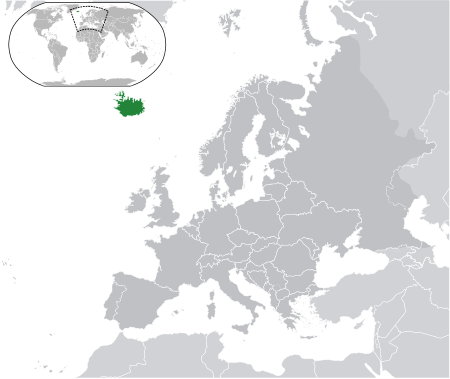
IslandiaÍsland (Islandia) Bendera Lambang Lagu kebangsaan: Lofsöngur (Himne Nasional Islandia) Perlihatkan BumiPerlihatkan peta EropaPerlihatkan peta BenderaLokasi Islandia (hijau gelap)di Eropa (abu-abu) Ibu kota(dan kota terbesar)Reykjavík64°8′N 21°56′W / 64.133°N 21.933°W / 64.133; -21.933Bahasa resmi dan bahasa nasionalIslandiaKelompok etnik (2018)[a][1]89% Islandia5% Polandia1% Lituania5…

Questa voce sull'argomento stagioni delle società calcistiche italiane è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Voce principale: Forlì Football Club. Associazione Calcio ForlìStagione 1950-1951Sport calcio Squadra Forlì Allenatore Antonio Budini Presidente Bruno Miserocchi Serie C5º posto nel girone B. 1949-1950 1951-1952 Si invita a seguire il modello di voce Questa voce raccoglie le info…

فاسيلي غيرغلي معلومات شخصية الميلاد 28 أكتوبر 1941 (83 سنة) بايا ماري الطول 1.72 م (5 قدم 7 1⁄2 بوصة) مركز اللعب وسط الجنسية رومانيا مسيرة الشباب سنوات فريق 1958–1960 ميناور بايا ماري [الإنجليزية] المسيرة الاحترافية1 سنوات فريق م. (هـ.) 1958–1962 ميناور بايا ما…

Pour les articles homonymes, voir Cocker. Joe CockerJoe Cocker au Festival du bout du monde en 2013.BiographieNaissance 20 mai 1944Sheffield (Angleterre)Décès 22 décembre 2014 (à 70 ans)Crawford (comté de Delta, Colorado, États-Unis)Sépulture Garden of Memories Cemetery (d)Nom de naissance John Robert CockerNationalité britanniqueDomicile CrawfordActivités Chanteur, pianiste, auteur-compositeur, acteur, artiste d'enregistrementPériode d'activité 1960-2014Conjoint Pam Baker (d)Aut…

Questa voce o sezione sull'argomento centri abitati della California non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento. Fresnocomune Fresno – Veduta LocalizzazioneStato Stati Uniti Stato federato California ConteaFresno AmministrazioneSindacoJerry P.Dyer (R) dal 5-1-2021 TerritorioCoordina…

Platìcomune Platì – Veduta LocalizzazioneStato Italia Regione Calabria Città metropolitana Reggio Calabria AmministrazioneSindacoRosario Sergi (lista civica) dal 22-9-2020 TerritorioCoordinate38°13′N 16°03′E / 38.216667°N 16.05°E38.216667; 16.05 (Platì)Coordinate: 38°13′N 16°03′E / 38.216667°N 16.05°E38.216667; 16.05 (Platì) Altitudine300 m s.l.m. Superficie50,87 km² Abitanti3 704[1] …

Professional wrestling tag team Professional wrestling tag team Big Show and KaneKane (left) and Big Show (right), during a WWE Live Event in 2016.Tag teamMembers Big Show KaneName(s)Big Show and KaneThe AuthorityBilled heights7 ft 0 in (2.13 m) each[1][2]Combinedbilled weight773 lb (351 kg)[1][2]DebutNovember 29, 2001DisbandedJuly 19, 2016Years active2001–20022005–200620112014–2016 Big Show and Kane were an American tag team active …





![{\displaystyle [a;b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/68e776d74130a8890a814c1f4e74372a9110d2f9)
![{\displaystyle {\overline {f(x)}}_{[a;b]}={\frac {1}{b-a}}\int _{a}^{b}f(x)dx.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/db0287956e28e4ced0b833809f5b0ed44aaa7339)











