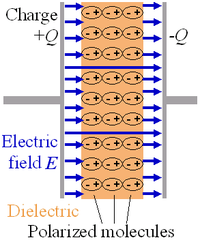
介電質 (英語:dielectric ,又称电介质 )是一種可被電極化 的絕緣體 。假設將介電質置入外電場 ,則束縛於其原子或分子的束縛電荷 不會流過介電質,只會從原本位置移動微小距離,即正電荷朝著電場方向稍微遷移,而負電荷朝著反方向稍微遷移。這會造成介電質電極化,從而產生反抗電場,減弱介電質內部的電場[ 1] 分子 構成,則這些分子不但會被電極化,也會改變取向 ,試著將自己的對稱軸與電場對齊[ 2]
介電質通常指的是可被高度電極化的物質。在原子與分子層次,極化性 可以用來衡量微觀的電極化性質,從極化性可以理論計算出介電質的電極化率 和電容率 ,兩個宏观的電極化性質。或者,可以直接從實驗測量出介電質的電極化率 和電容率 。假若置入了具有高電容率的介電質,則平行板電容器 的電容 會大幅增加,儲存於兩塊金屬平行板的正負電荷也會增加[ 2] 介电常数 κ。假如一种绝缘体充满两个平行板电容器 之间会使得该电容器的电容增加κ 倍,该绝缘体的介电常数则为κ。该电介质特性完全由该绝缘体本身的性质所决定,与外加的电场无关。[ 3]
介電質的用途相當廣泛。介電質的電傳導 能力很低,再加上具備有很好的介電強度 (dielectric strength )性質,就可以用來製造電絕緣體。另外介電質可被高度電極化,是優良的電容器材料。對於介電性質的研究,涉及了物質內部電能和磁能的儲存與耗散[ 4] 電子學 、光學 和固態物理 的各種各樣現象,這研究極端重要。
回應麥可·法拉第 的請求,英國科學家威廉·暉巍 (William Whewell )命名所有可被電極化的絕緣體為介電質[ 5]
介電質因響應外電場 的施加而極化 的程度,可以用電極化率來衡量。從電極化率又可以計算出介電質的電容率 。因此,電極化率會影響介電質內各種其它可能發生的現象,像電容器 的電容 、光波 傳播於物質內部的光速 等等。
對於各向同性 、線性 、均勻的介電質,電極化率
χ
e
{\displaystyle \chi _{e}}
P
=
d
e
f
ϵ
0
χ
e
E
{\displaystyle \mathbf {P} \ {\stackrel {def}{=}}\ \epsilon _{0}\chi _{e}\mathbf {E} }
其中,
E
{\displaystyle \mathbf {E} }
電場 ,
P
{\displaystyle \mathbf {P} }
電極化強度 ,
ϵ
0
{\displaystyle \epsilon _{0}}
電常數 (或称为真空电容率 )。
由於電位移
D
{\displaystyle \mathbf {D} }
D
=
d
e
f
ϵ
0
E
+
P
{\displaystyle \mathbf {D} \ {\stackrel {\mathrm {def} }{=}}\ \epsilon _{0}\mathbf {E} +\mathbf {P} }
所以,電位移與電場成正比:
D
=
ϵ
0
(
1
+
χ
e
)
E
=
ϵ
E
{\displaystyle \mathbf {D} =\epsilon _{0}(1+\chi _{e})\mathbf {E} =\epsilon \mathbf {E} }
其中,
ϵ
{\displaystyle \epsilon }
電容率 。
定義相對電容率
ϵ
r
{\displaystyle \epsilon _{r}}
ϵ
r
=
d
e
f
ϵ
/
ϵ
0
{\displaystyle \epsilon _{r}\ {\stackrel {\mathrm {def} }{=}}\ \epsilon /\epsilon _{0}}
那麼,介電質的電極化率與相對電容率的關係式為
χ
e
=
ϵ
r
−
1
{\displaystyle \chi _{e}\ =\epsilon _{r}-1}
在自由空間 裏,
χ
e
=
0
{\displaystyle \chi _{e}\ =0}
假若介電質具有各向異性 ,則電極化率是一個二階張量 。
一般而言,物質無法為了要響應一個含時外電場的變化而瞬時地電極化。因此,更廣義的表述必須將時間
t
{\displaystyle t}
P
(
t
)
=
ϵ
0
2
π
∫
−
∞
t
χ
e
(
t
−
t
′
)
E
(
t
′
)
d
t
′
{\displaystyle \mathbf {P} (t)={\frac {\epsilon _{0}}{\sqrt {2\pi }}}\int _{-\infty }^{t}\chi _{e}(t-t')\mathbf {E} (t')\,dt'}
那就是,電極化強度是先前時間的電場與含時電極化率
χ
e
(
Δ
t
)
{\displaystyle \chi _{e}(\Delta t)}
摺積 。假設每當
Δ
t
=
t
−
t
′
<
0
{\displaystyle \Delta t=t-t'<0}
χ
e
(
Δ
t
)
=
0
{\displaystyle \chi _{e}(\Delta t)=0}
P
(
t
)
=
ϵ
0
2
π
∫
−
∞
∞
χ
e
(
t
−
t
′
)
E
(
t
′
)
d
t
′
{\displaystyle \mathbf {P} (t)={\frac {\epsilon _{0}}{\sqrt {2\pi }}}\int _{-\infty }^{\infty }\chi _{e}(t-t')\mathbf {E} (t')\,dt'}
瞬時的響應對應於狄拉克δ函數 電極化率
χ
e
(
Δ
t
)
=
χ
e
δ
(
Δ
t
)
{\displaystyle \chi _{e}(\Delta t)=\chi _{e}\delta (\Delta t)}
對於一個線性系統,可以簡單地做一個傅立葉變換 ,將這關係式寫為頻率
ω
{\displaystyle \omega }
P
(
ω
)
=
1
2
π
∫
−
∞
∞
P
(
t
)
e
i
ω
t
d
t
=
ϵ
0
2
π
∫
−
∞
∞
[
∫
−
∞
∞
χ
e
(
t
−
t
′
)
E
(
t
′
)
d
t
′
]
e
i
ω
t
d
t
=
ϵ
0
2
π
∫
−
∞
∞
[
∫
−
∞
∞
χ
e
(
t
−
t
′
)
e
i
ω
(
t
−
t
′
)
d
t
]
E
(
t
′
)
e
i
ω
t
′
d
t
′
=
ϵ
0
2
π
∫
−
∞
∞
[
∫
−
∞
∞
χ
e
(
t
″
)
e
i
ω
(
t
″
)
d
t
″
]
E
(
t
′
)
e
i
ω
t
′
d
t
′
=
ϵ
0
2
π
[
∫
−
∞
∞
χ
e
(
t
″
)
e
i
ω
(
t
″
)
d
t
″
]
[
∫
−
∞
∞
E
(
t
′
)
e
i
ω
t
′
d
t
′
]
=
ϵ
0
χ
e
(
ω
)
E
(
ω
)
{\displaystyle {\begin{aligned}\mathbf {P} (\omega )&={\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{\infty }\mathbf {P} (t)e^{i\omega t}\,dt\\&={\frac {\epsilon _{0}}{2\pi }}\int _{-\infty }^{\infty }\left[\int _{-\infty }^{\infty }\chi _{e}(t-t')\mathbf {E} (t')\,dt'\right]e^{i\omega t}\,dt\\&={\frac {\epsilon _{0}}{2\pi }}\int _{-\infty }^{\infty }\left[\int _{-\infty }^{\infty }\chi _{e}(t-t')e^{i\omega (t-t')}\,dt\right]\mathbf {E} (t')e^{i\omega t'}\,dt'\\&={\frac {\epsilon _{0}}{2\pi }}\int _{-\infty }^{\infty }\left[\int _{-\infty }^{\infty }\chi _{e}(t'')e^{i\omega (t'')}\,dt''\right]\mathbf {E} (t')e^{i\omega t'}\,dt'\\&={\frac {\epsilon _{0}}{2\pi }}\left[\int _{-\infty }^{\infty }\chi _{e}(t'')e^{i\omega (t'')}\,dt''\right]\left[\int _{-\infty }^{\infty }\mathbf {E} (t')e^{i\omega t'}\,dt'\right]\\&=\epsilon _{0}\chi _{e}(\omega )\mathbf {E} (\omega )\\\end{aligned}}}
。 這結果是摺積定理 的一個範例。
在頻率空間,電極化強度與電場成正比,比例為電極化率乘以電常數。從電極化率的頻率函數,可以描繪出物質的色散 性質。
由於因果關係 ,電極化只能跟先前時間的電場有關(也就是說,每當
Δ
t
<
0
{\displaystyle \Delta t<0}
χ
e
(
Δ
t
)
=
0
{\displaystyle \chi _{e}(\Delta t)=0}
χ
e
(
0
)
{\displaystyle \chi _{e}(0)}
克拉莫-克若尼約束 。
介電質大致分為兩類[ 6] :55ff :
非極性介電質(中性电介质):每一個分子的負電荷的質心位置與正電荷的質心位置相同。假設外電場為零,則每一個分子的電偶極矩為零。包括:单原子分子He(氦)、相同原子组成的双原子分子H2 (氢气)、O2 (氧气)、对称分布的多原子分子CH4 (甲烷)等等。其特点为导电能力较低、损耗小、不易发生热击穿。例如:变压器油、聚乙烯塑料。 極性介電質:每一個分子的負電荷的質心位置與正電荷的質心位置不相同。每一個分子都單獨具有電偶極矩。但是,由於電偶極矩是隨機的,整個介電質的平均電偶極矩為零。包括,H2 O(水)、NH3 (氨)、SO2 (二氧化硫)等等。其特点为导电能力较强、损耗大、易发热、发生热击穿。例如:天然橡胶、酚醛树脂。弱极性电介质:电偶极矩μ 0 ≤0.5D(德拜,电偶极距的单位);中极性:0.5<μ 0 ≤1.5D;强极性:μ 0 ≥1.5D。 离子型电介质:由离子键形成的电介质。例如:无机玻璃、云母、石英。
同一種介電質可能會涉及到幾種不同的電極化機制,每一種電極化機制都有其主要活動頻率,都有其特徵的截止頻率,超過這截止頻率,對應的機制無法跟著電磁波振動,不再能貢獻出電極化。對於每一種介電質,電極化機制的截止頻率與電極化程度都不相同。[ 7]
按照經典介電質模型,原子是由帶負電荷的電子雲環繞著位於中心、帶正電荷的原子核所組成。 感受到外電場的作用,原子核會朝著外電場方向遷移位置,而電子雲則會朝著反方向遷移位置。
如左圖所示,按照經典介電質模型,物質內部的每一個原子 ,都是由帶負電荷的電子雲和位於電子雲中心、帶正電荷的原子核所組成。假設將物質置入於外電場,則由於外電場的作用,正電荷會朝著外電場方向遷移位置,而負電荷則會朝著反方向遷移位置。正電荷與負電荷的相對位移會形成電偶極矩,這現象稱為「電子極化」(electronic polarization )。由於外電場與電偶極矩的耦合,從而給出介電質的物理行為。像氦氣 、氖氣 等等一類的惰性氣體 最能展示出電子極化性質。假設將外電場關閉,則原子會回返原來狀態。這過程所需要的時間稱為弛豫時間 (relaxation time )。[ 6] :56-58 [ 8] :68
介電質的物理行為是由電場
E
{\displaystyle \mathbf {E} }
p
{\displaystyle \mathbf {p} }
p
=
p
(
E
)
{\displaystyle \mathbf {p} =\mathbf {p} (\mathbf {E} )}
折射率 、色散 、雙折射 、自聚焦 (self-focusing )、諧波產生 (harmonic generation )。
假設外電場為零,離子晶體 內部離子 整齊有規律的交替排列。 假設外電場不為零,正離子與負離子之間的相對位移會形成離子極化。
離子晶體 中含有電荷量相等的陰離子 和陽離子 ,並且這兩種離子 交替排列,整齊有規律,往往呈現出規則的幾何外形。比如:氯化鈉 晶體呈現出立方體的空間構型,每個钠离子周圍有上下前後左右共6個最近的等距離的氯离子;每個氯离子周圍有上下前後左右共6個最近的等距離的钠离子。在正常狀況,假設外電場為零,則巨觀電偶極矩為零。但是,假設外電場不為零,則由於正離子會朝著外電場方向遷移位置,而負離子則會朝著反方向遷移位置。正離子與負離子之間的相對位移形成了「離子極化」(ionic polarization ),又稱為「原子極化」(atomic polarization)巨觀電偶極矩不等於零。例如,氯化鈉 、氯化鉀 等等。[ 6] :59 [ 8] :68
假設外電場為零,介電質內部的極性分子的取向。 假設外電場不為零,介電質內部的極性分子的取向。
「取向極化」(orientation polarization )是一種特別的電極化,只出現於極性分子 ,又稱為「二極性極化」(dipolar polarization)。這種電極化是由永久電偶極子 的取向改變而產生。例如,氧原子 與氫原子 之間的非對稱鍵。雖然在外電場為零的狀況,每一個單獨永久電偶極子仍具有極性 。對於介電質內部任意位置,設定以此位置為中心的尺度夠大的區域,將其內部所有電偶極矩的總合除以區域的體積,則可得到在這位置的巨觀電極化強度。[ 6] :59-60 [ 8] :68
假設施加非零外電場於此介電質,雖然正電荷與負電荷之間的距離,由於跟化學鍵 有關,大致會保持不變,但是,感受到外電場的力矩,電偶極子會旋轉,趨向於外電場的方向,從而增加巨觀電極化強度。
這旋轉過程發生的時間尺度與力矩和周圍的局域黏滯性 有關。這旋轉過程不是瞬時的,由於在時間方面的延遲,假設電場的變化頻率足夠高,介電質會失去響應的能力。另外,電偶極子的旋轉運動會造成摩擦 和發熱。水分子 能夠微波 加熱就是應用這效應。
處於電場的介電質,其內部的電荷載子可能會遷移一段距離,假若這些電荷載子的遷移運動被阻礙,例如在非均質材料的結構界面,由於電荷累積,會發生「界面極化」(interfacial polarization)現象。很多種陶瓷材料都會發生界面極化現象,特別是當處於高溫狀況。[ 6] :60-61
上述幾種電極化機制並不互相排斥。介電質的總電極化強度是所有可能電極化機制的總合。非均質介電質的總電極化強度
P
T
{\displaystyle \mathbf {P} _{T}}
[ 6] :61
P
T
=
P
e
+
P
o
+
P
a
+
P
s
{\displaystyle \mathbf {P} _{T}=\mathbf {P} _{e}+\mathbf {P} _{o}+\mathbf {P} _{a}+\mathbf {P} _{s}}
其中,
P
e
{\displaystyle \mathbf {P} _{e}}
P
o
{\displaystyle \mathbf {P} _{o}}
P
a
{\displaystyle \mathbf {P} _{a}}
P
s
{\displaystyle \mathbf {P} _{s}}
均質介電質的總電極化強度
P
T
{\displaystyle \mathbf {P} _{T}}
P
T
=
P
e
+
P
o
+
P
a
{\displaystyle \mathbf {P} _{T}=\mathbf {P} _{e}+\mathbf {P} _{o}+\mathbf {P} _{a}}
對於像氦氣、氖氣一類的非極性介電質,由於沒有離子鍵 ,
P
T
=
P
e
{\displaystyle \mathbf {P} _{T}=\mathbf {P} _{e}}
對於像氯化鈉、氯化鉀一類的離子晶體,由於在正常狀況,取向極化強度為零,所以
P
T
=
P
e
+
P
a
{\displaystyle \mathbf {P} _{T}=\mathbf {P} _{e}+\mathbf {P} _{a}}
涵蓋寬廣頻域的介電質的電容率頻譜。
ϵ
′
{\displaystyle \epsilon '}
ϵ
″
{\displaystyle \epsilon ''}
[ 7] 由於含時外電場的作用,介電質內部的帶電粒子會遷移位置。但是,這動作需要時間來完成。所以,對於外電場的變化,響應的電極化在時間方面必定會有所推遲。這意味著牽涉到的電極化機制密切地跟外電場的頻率有關:[ 6] :81-82 :
由於電荷載子需要時間移動幾個原子距離,界面極化是很慢的程序,發生於電功率 頻率,大約為50-60赫茲。
取向極化與分子電偶極子的慣性有關,在較高頻率仍舊能產生。可是在微波頻域內,頻率高達大約108 赫茲 時,取向極化開始無法跟隨含時外電場。
離子極化是因離子位移而產生的現象。在紅外線 或遠紅外線 頻域,頻率高達大約1013 赫茲時,離子極化失去響應含時外電場的能力。
電子極化涉及到電子的運動,比離子輕很多,可以快捷運動,但在紫外線 頻域,頻率高達大約1015 赫茲時,電子極化不再能夠響應含時外電場。 假設緩慢地調高頻率,這些極化現象會一個接著一個的消失,電容率的趨勢也會越來越低。在頻率大於紫外線 的頻域,電極化率趨向於零,電容率趨向於電常數
ϵ
0
{\displaystyle \epsilon _{0}}
離子導電現象會對介電損耗
ϵ
r
″
{\displaystyle \epsilon _{r}''}
溶劑 ,其內部的自由離子會出現電解傳導效應,這稱為「離子導電」(ionic conduction),對介電損耗的影響,以方程式表示為
σ
/
ω
ϵ
0
{\displaystyle \sigma /\omega \epsilon _{0}}
σ
{\displaystyle \sigma }
電導率 ,
ω
{\displaystyle \omega }
[ 7]
∇
⋅
E
=
ρ
ϵ
0
=
ρ
p
o
l
a
r
i
z
e
d
+
ρ
o
t
h
e
r
ϵ
0
=
ρ
o
t
h
e
r
ϵ
0
−
1
ϵ
0
∇
⋅
P
{\displaystyle \nabla \cdot \mathbf {E} ={\frac {\rho }{\epsilon _{0}}}={\frac {\rho _{polarized}+\rho _{other}}{\epsilon _{0}}}={\frac {\rho _{other}}{\epsilon _{0}}}-{\frac {1}{\epsilon _{0}}}\nabla \cdot \mathbf {P} }
c
2
∇
×
B
=
j
ϵ
0
+
∂
E
∂
t
=
j
o
t
h
e
r
ϵ
0
+
j
p
o
l
a
r
i
z
e
d
ϵ
0
+
∂
E
∂
t
{\displaystyle c^{2}\nabla \times \mathbf {B} ={\frac {\mathbf {j} }{\epsilon _{0}}}+{\frac {\partial \mathbf {E} }{\partial t}}={\frac {\mathbf {j_{other}} }{\epsilon _{0}}}+{\frac {\mathbf {j_{polarized}} }{\epsilon _{0}}}+{\frac {\partial \mathbf {E} }{\partial t}}}
电位移 的定义为
D
=
ϵ
0
E
+
P
{\displaystyle \mathbf {D} =\epsilon _{0}\mathbf {E} +\mathbf {P} }
∇
⋅
D
=
ρ
o
t
h
e
r
{\displaystyle \nabla \cdot \mathbf {D} =\rho _{other}}
ϵ
0
c
2
∇
×
B
=
j
o
t
h
e
r
+
∂
D
∂
t
{\displaystyle \epsilon _{0}c^{2}\nabla \times \mathbf {B} =\mathbf {j_{other}+{\frac {\partial \mathbf {D} }{\partial t}}} }
式子中的
ρ
p
o
l
a
r
i
z
e
d
{\displaystyle \rho _{polarized}}
ρ
o
t
h
e
r
{\displaystyle \rho _{other}}
其余两个方程则为
∇
×
E
=
−
∂
B
∂
t
{\displaystyle \nabla \times \mathbf {E} =-{\frac {\partial \mathbf {B} }{\partial t}}}
∇
⋅
B
=
0
{\displaystyle \nabla \cdot \mathbf {B} =0}
介電質內部的正束縛電荷與負束縛電荷會分別朝著電場方向與反方向遷移位置。這會有效地降低總電場。(空氣空隙為幫助顯示用,實際的介電質是與平行板直接接觸的。) 使用介電質材料最顯著的優點是,能夠防止兩塊分別儲存正負電荷的平行板互相發生接觸,從而造成短路 。更重要的原因是,給定電壓
V
{\displaystyle V}
Q
{\displaystyle Q}
Q
=
ϵ
A
V
/
d
{\displaystyle Q=\epsilon AV/d}
其中,
A
{\displaystyle A}
d
{\displaystyle d}
由於電容
C
{\displaystyle C}
C
=
Q
/
V
=
ϵ
A
/
d
{\displaystyle C=Q/V=\epsilon A/d}
給定電壓,電容率越高,儲存於平行板電荷量也變得越大,電容也會增高。
另外,製作電容器的介電質材料必需能夠抵抗電離作用 。這性質允許電容器能夠在更高電壓運作,不會過早因為電離作用而出現電流。
球形共振器。 圓柱形共振器。 介電質共振器(orientation polarization )是一種電子元件,能夠造成在狹窄頻域內的共振,通常這狹窄頻域為微波頻帶。介電質共振器的介電質材料是高電容率與低耗散因子 (dissipation factor )的陶瓷 。這種共振器時常用為震盪電路的頻率參考。無屏蔽介電質共振器可以用為介電質共振器天線 (dielectric resonator antenna )[ 9]
介電質可以是固體,液體,或氣體。另外,高真空也是一種有用、無損失的介電質,雖然其相對電容率 僅為1。
固態介電質被廣泛使用於電子工業,是非常優良的絕緣體,例如瓷器 、玻璃 、大多數種類的塑膠 。三種最廣泛使用的氣態介電質 (gaseous dielectric )為空氣、氮氣 與六氟化硫 。
聚對二甲苯 可以用為工業鍍膜 (industrial coating ),提供基質與外界環境之間的介電質障壁。礦物油 (mineral oil )廣泛地使用於變壓器 。對於這用途,礦物油的主要功能為液態介電質與協助散熱。具有高電容率 的介電質液體,像電子工業用蓖麻油 ,常被注入高電壓電容器 中來協助防止電暈放電 (corona discharge ),並可提高電容。由於介電質阻礙電流流動,介電質表面或許會存留著停滯不動的多於電荷。這可能是因為摩擦介電質而意外造成的效應(摩擦起電效應 )。范德格拉夫起電機 與起電盤 (electrophorus )就是應用這種效應運作。但是,這效應也可能會因為靜電放電 而造成電子元件的損壞。
駐極體 是一種特別的介電質,具有半永久的電荷或電極化強度。駐極體能夠產生電場,就好像磁鐵 能夠產生磁場 一樣。駐極體可以用來製作傳聲器、揚聲器、耳機、觸摸面板等等。當感受到機械壓力時,某些介電質會產生電壓差;或者當施加外電壓於這些介電質兩端時,這些介電質會改變物理形狀。這效應稱為壓電效應 。具有這種特性的介電質可以用來製造打火機 、感測器 、致動器 、晶體諧振器 等等。
有些離子晶體 或聚合物 擁有自發性電極化;施加外電場可以逆反這自發性電極化。這種物理行為稱為鐵電性 效應,類似靜磁學 的鐵磁性 物質感受到外磁場作用所表現出的物理行為。鐵電性介電質可以用來製作可調的電容器 、鐵電隨機存取記憶體 、感測器等等。
^ Dielectric (页面存档备份 ,存于互联网档案馆 ). Encyclopedia Britannica^ 2.0 2.1
Dielectrics (physics). Britannica: 1. 2009. Online.
^ 费恩曼; 莱顿,桑兹. 费恩曼物理学讲义第2卷. 上海科学技术出版社. 2005年: 122. ^ 美國物理學者Arthur R. von Hippel,在他的權威著作《介電性物質與應用》(Dielectric Materials and Applications )裏闡明,「介電質不是一種狹義的所謂絕緣體,而是從它們與電場、磁場、電磁場交互作用的觀點來思考的廣泛範圍的非金屬,包括氣態、液態、固態物質,以及電能和磁能的儲存和耗散。」(Technology Press of MIT and John Wiley, NY, 1954).
^ J. Daintith. Biographical Encyclopedia of Scientists. CRC Press. 1994: 943. ISBN 0750302879 ^ 6.0 6.1 6.2 6.3 6.4 6.5 6.6 Maheshwari, Preeti, Electronic Components And Processes, New Age International, 2008, ISBN 9788122417944 ^ 7.0 7.1 7.2 Agilent Basics of Measuring the Dielectric Prop[erties of Materials (PDF) . Agilent Technologies Inc. [2013-09-22 ] . (原始内容 (PDF) 存档于2013-09-26). ^ 8.0 8.1 8.2 Hecht, Eugene, Optics 4th, United States of America: Addison Wesley, 2002, ISBN 0-8053-8566-5(英语) ^ Chen, LinFen, Microwave electronics: measurement and materials characterization illustrated, John Wiley and Sons: pp. 103ff, 2004, ISBN 9780470844922
























![{\displaystyle {\begin{aligned}\mathbf {P} (\omega )&={\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{\infty }\mathbf {P} (t)e^{i\omega t}\,dt\\&={\frac {\epsilon _{0}}{2\pi }}\int _{-\infty }^{\infty }\left[\int _{-\infty }^{\infty }\chi _{e}(t-t')\mathbf {E} (t')\,dt'\right]e^{i\omega t}\,dt\\&={\frac {\epsilon _{0}}{2\pi }}\int _{-\infty }^{\infty }\left[\int _{-\infty }^{\infty }\chi _{e}(t-t')e^{i\omega (t-t')}\,dt\right]\mathbf {E} (t')e^{i\omega t'}\,dt'\\&={\frac {\epsilon _{0}}{2\pi }}\int _{-\infty }^{\infty }\left[\int _{-\infty }^{\infty }\chi _{e}(t'')e^{i\omega (t'')}\,dt''\right]\mathbf {E} (t')e^{i\omega t'}\,dt'\\&={\frac {\epsilon _{0}}{2\pi }}\left[\int _{-\infty }^{\infty }\chi _{e}(t'')e^{i\omega (t'')}\,dt''\right]\left[\int _{-\infty }^{\infty }\mathbf {E} (t')e^{i\omega t'}\,dt'\right]\\&=\epsilon _{0}\chi _{e}(\omega )\mathbf {E} (\omega )\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ffcc0027cfa9a8c6bba962adadc99ce25be38df4)







































