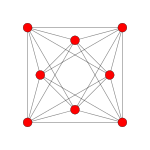
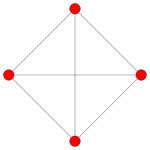
正十六胞体 (Hexadecachoron)是数学家施莱夫利 最先发现的六个四维凸正多胞体 之一。它是四维的正轴形 ,是二维正方形 、三维正八面体 的类比。同时,它还是四维的半超方形 ,即半超正方体。
正十六胞体由十六个正四面体 胞组成。其24条棱组成6个在不同坐标平面的正方形,它们互相正交 ;也能组成4个在不同三维超平面上的正八面体,也互相正交。
作为四维正轴形,正十六胞体的八个顶点坐标是正十六胞体堆砌 ,施莱夫利符号{3,3,4,3}。它由16个正四面体 胞、32个正三角形面、24条棱、8个顶点组成,棱图是正方形 ,顶点图 是正八面体。对于边长为a的正十六胞体,其超体积为
a
4
6
{\displaystyle {\frac {a^{4}}{6}}}
4
2
a
3
3
{\displaystyle {\frac {4{\sqrt {2}}a^{3}}{3}}}
对于边长为a的正十六胞体,其外接超球半径为
2
2
≈
0.7071067812
{\displaystyle {\frac {\sqrt {2}}{2}}\approx 0.7071067812}
1
2
{\displaystyle {\frac {1}{2}}}
6
6
≈
0.4082482905
{\displaystyle {\frac {\sqrt {6}}{6}}\approx 0.4082482905}
2
4
≈
0.3535533906
{\displaystyle {\frac {\sqrt {2}}{4}}\approx 0.3535533906}
作为四维正轴形,它具有C4 对称群,但它同时也是四维的半超方形 (可看作以一定规律选取超方形 一半的顶点构成新的半正多胞形,见交错 ),对应施莱夫利符号h{4,3,3},考斯特标记反棱柱 ,即由两个以对偶形式存在的互相平行 的正四面体和链接它们顶点和面的正四面体组成,施莱夫利符号h0,1 {2,4,3}其对称性更低。也因为其对偶超立方体 是四角四角柱體柱 ,它也是四角四角錐體錐 交错 ,它也是四角四角反柱體反柱
对应名称
考克斯特符号 施莱夫利符号
对称性 群阶
顶点图
正十六胞体
{3,3,4}
[3,3,4]
384
半超正方体
h{4,3,3}1,1 }
[31,1,1 ] = [1+ ,4,3,3]
192
四角四角錐體錐
{4}+{4}
[[4,2,4]]
128
交错 四角四角柱體柱
2s{4,2,4}
[[4,2+ ,4]]
64
正四面体反棱柱
s{2,4,3}
[3,4,2+ ]
48
交错四角柱體柱
[4,2+ ,4]
32
交错正方形棱柱棱柱
sr{2,2,4}
[4,(2,2)+ ]
16
扭棱四维超矩形
s{21,1,1 }
[23 ]+
8
4-长菱体
{3,3,4}
[3,3,4]
384
{4}+{4}
[[4,2,4]]
128
{3,4}+{}
[4,3,2]
96
{4}+{}+{}
[4,2,2]
32
{}+{}+{}+{}
[2,2,2]
16
球极投影 展开图(这里显示了正十六胞体作为
单旋转着的透视投影
正交投影
考克斯特平面 B4
B3 / D4 / A2
B2 / D3
图像
二面体对称群
[8]
[6]
[4]
考克斯特平面
F4
A3
图像
二面体对称群
[12/3]
[4]
正十六胞体堆砌 正十六胞体可以獨立密铺 四维欧氏空间,这个密铺被叫做正十六胞体堆砌 ,有施莱夫利符号{3,3,4,3},它的对偶四维砌——正二十四胞体堆砌 ,{3,4,3,3},是正二十四胞体 的四维欧氏空间密铺。再加上超正方体堆砌 ,{4,3,3,4},这就是四维欧几里得空间 R 4 中唯一的3个凸正密铺。每个正十六胞体都与16个相邻的正十六胞体四维胞共用一个四面体胞,与24个相邻的四维胞共用一条棱,与72个相邻的四维胞共用一个顶点。每个顶点处都有24个正十六胞体相交,因此,正十六胞体堆砌的顶点图是正十二胞体。
正十六胞体投影的凸包,不同的胞被涂上了不同的颜色,后半面的胞未画出。 正十六胞体到三维的正对胞的平行 投影 有着立方体 形的凸包,最近的和最远的(从四维视角来看)正四面体胞被投影成了立方体的内接四面体,正好对应于将正四面体内接于立方体的两种不同方式。在每个这样的内接正四面体周围是4个(非正的)四面体,即是与最近的和最远的正四面体胞相邻的正四面体胞的投影,填充了内接正四面体与立方体之间的空隙。剩余的6个胞被投影成了立方体的6个正方形面。在这一投影中,正十六胞体所有的棱都位于投影的凸包上。
正十六胞体到三维的正对胞的透视投影 有着三角化正四面体 凸包,其内部结构与平行投影相似。
正十六胞体到三维的正对顶点的平行 投影 有着正八面体 形的凸包,正八面体能够被其“坐标平面”划分为8个四面体部分,这里每一个四面体都是远近一对正四面体胞的投影,距离四维视角最远和最近的顶点都被投影成了正八面体的中心。
最后,正十六胞体到三维的正对棱的平行投影有着压扁的八面体的凸包;正对面的平行投影有一个六角双棱锥 凸包。
正十六胞体通常的球极投影 维恩图 ),在拓扑 上是三维空间中的同一物体:
T. Gosset On the Regular and Semi-Regular Figures in Space of n Dimensions , Messenger of Mathematics, Macmillan, 1900H.S.M. Coxeter :
Coxeter, Regular Polytopes ISBN 0-486-61480-8 , p.296, Table I (iii): Regular Polytopes, three regular polytopes in n-dimensions (n≥5)
H.S.M. Coxeter, Regular Polytopes , 第三版, Dover New York, 1973, p.296, Table I (iii): Regular Polytopes, three regular polytopes in n-dimensions (n≥5)
Kaleidoscopes: Selected Writings of H.S.M. Coxeter ,F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication参与修改, 1995, ISBN 978-0-471-01003-6 [1] (页面存档备份 ,存于互联网档案馆 )
(22页) H.S.M. Coxeter, Regular and Semi Regular Polytopes I , [Math. Zeit. 46 (1940) 380-407, MR 2,10]
(23页) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II , [Math. Zeit. 188 (1985) 559-591]
(24页) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III , [Math. Zeit. 200 (1988) 3-45] John H. Conway , Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (26章.409页: Hemicubes: 1n1 )Norman Johnson Uniform Polytopes , Manuscript (1991)
N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs , Ph.D. (1966) Regular Convex Four-Dimensional Polytopes 提供了正十六胞体的部分几何数据。
四维正多胞体
正五胞体 超立方体 正十六胞体 正二十四胞体 正一百二十胞体 正六百胞体
{3,3,3}
{4,3,3}
{3,3,4}
{3,4,3}
{5,3,3}
{3,3,5}