Axiom schema of specification
|

BESIX Group S.A.JenisSociété AnonymeIndustriKonstruksiDidirikan1909; 115 tahun lalu (1909)KantorpusatBrussels, BelgiaWilayah operasiSeluruh duniaTokohkunciRik Vandenberghe (CEO), Johan Beerlandt (Chairman)JasaKonstruksi, Pengembangan Lahan Yasan, Konsesi & AsetPendapatan €3,33 milyar (2019)PemilikOrascom Construction (50%), Masyarakat Belgia (50%)Karyawan14.000 (2017)Situs webwww.besix.com BESIX Group adalah sebuah perusahaan konstruksi yang berkantor pusat di Brussels,[1] d…

Katedral ZacatecasKatedral Basilika Bunda Maria Diangkat ke SurgaSpanyol: Catedral Basílica de la Asunción de María de Zacatecascode: es is deprecated Katedral ZacatecasLokasiZacatecasNegaraMeksikoDenominasiGereja Katolik RomaArsitekturStatusKatedralStatus fungsionalAktifAdministrasiKeuskupanKeuskupan Zacatecas Katedral Zacatecas, yang bernama lengkap Katedral Basilika Bunda Maria Diangkat ke Surga (Spanyol: Catedral Basílica de la Asunción de María de Zacatecascode: es is deprecated ) ada…

John Jay Gubernur New York KeduaMasa jabatan1 Juli 1795 – 30 Juni 1801WakilStephen Van Rensselaer PendahuluGeorge ClintonPenggantiGeorge ClintonKetua Mahkamah Agung Amerika Serikat PertamaMasa jabatan19 Oktober 1789 – 29 Juni 1795Ditunjuk olehGeorge Washington PendahuluJabatan didirikanPenggantiJohn RutledgeSekretaris Urusan Luar Negeri Amerika Serikat KeduaMasa jabatan7 Mei 1784 – 22 Maret 1790Ditunjuk olehKongres Konfederasi PendahuluRobert LivingstonPenggantiT…

本條目存在以下問題,請協助改善本條目或在討論頁針對議題發表看法。 此條目需要补充更多来源。 (2018年3月17日)请协助補充多方面可靠来源以改善这篇条目,无法查证的内容可能會因為异议提出而被移除。致使用者:请搜索一下条目的标题(来源搜索:羅生門 (電影) — 网页、新闻、书籍、学术、图像),以检查网络上是否存在该主题的更多可靠来源(判定指引)。 此�…

SungaiambangKelurahanNegara IndonesiaProvinsiRiauKotaPekanbaruKecamatanRumbai TimurKodepos28292Kode Kemendagri14.71.15.1003 Kode BPS1471081007 Luas29.78 km² (2021)Jumlah penduduk1370 Jiwa (2021)Kepadatan... jiwa/km² Sungaiambang adalah salah satu kelurahan di Kecamatan Rumbai Timur, Kota Pekanbaru, Provinsi Riau, Indonesia. Kelurahan ini dibentuk dari wilayah Kelurahan Lembah Damai dalam pemekaran wilayah di Kota Pekanbaru tahun 2016.[1] Menurut data dari Kelurahan Sungaiambang, t…

العلاقات البرتغالية الليختنشتانية البرتغال ليختنشتاين البرتغال ليختنشتاين تعديل مصدري - تعديل العلاقات البرتغالية الليختنشتانية هي العلاقات الثنائية التي تجمع بين البرتغال وليختنشتاين.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة وم…

Kijing Kijing air tawar Klasifikasi ilmiah Kerajaan: Animalia Filum: Mollusca Kelas: Bivalvia Subkelas: Palaeoheterodonta Ordo: Unionida Superfamili: Unionoidea Famili: Unionidae Subfamili: Gonideinae Tribus: Pseudodontini Subtribus: Pilsbryoconchina Genus: Pilsbryoconcha Spesies: Pilsbryoconcha exilisI.Lea, 1838 Kijing atau Remis adalah nama sejenis kerang yang hidup di sungai. Di seputaran danau Sentarum, Kapuas Hulu, dinamai kedungkang. Kijing sangat suka mengendap di dasar sungai yang berpas…

فورهيسفيل الإحداثيات 42°38′59″N 73°55′45″W / 42.649722222222°N 73.929166666667°W / 42.649722222222; -73.929166666667 [1] تقسيم إداري البلد الولايات المتحدة[2] التقسيم الأعلى مقاطعة ألباني خصائص جغرافية المساحة 5.551827 كيلومتر مربع5.551723 كيلومتر مربع (1 أبريل 2010) ارتفاع 103 …

artikel ini perlu dirapikan agar memenuhi standar Wikipedia. Tidak ada alasan yang diberikan. Silakan kembangkan artikel ini semampu Anda. Merapikan artikel dapat dilakukan dengan wikifikasi atau membagi artikel ke paragraf-paragraf. Jika sudah dirapikan, silakan hapus templat ini. (Pelajari cara dan kapan saatnya untuk menghapus pesan templat ini) Dory Funk Jr.Funk pada tahun 1973Nama lahirDorrance Earnest FunkLahir3 Februari 1941 (umur 83)[1][2][3]Hammond, Indiana,…

La population mondiale en juin 2014 est d'environ 7,2 milliards d'individus[1]. Une décroissance démographique, un déclin démographique, ou, plus anciennement, une dépopulation, est, pour une zone ou un pays donné, une situation dans laquelle le nombre d’habitants diminue. Les causes peuvent être un taux de mortalité supérieur au taux de natalité, ou des flux d’émigration nets supérieurs à l’accroissement naturel. Ces flux migratoires peuvent être induits par des guerres, des…
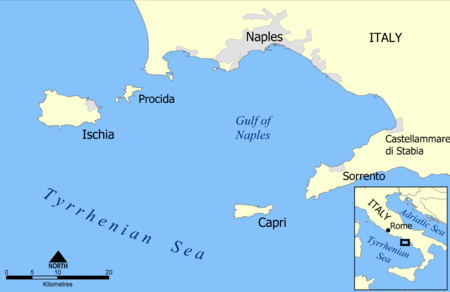
Volcanic island in the Tyrrhenian Sea For other uses, see Ischia (disambiguation). This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Ischia – news · newspapers · books · scholar · JSTOR (January 2018) (Learn how and when to remove this template message) IschiaView of Ischia from ProcidaHighest pointElevation…

Attorney General of New HampshireIncumbentJohn Formellasince April 22, 2021New Hampshire Department of JusticeTypeAttorney GeneralAppointerGovernor of New Hampshirewith approval of the Governor's CouncilTerm length4 yearsConstituting instrumentPart II, Article 46 of the Constitution of New HampshireFormation1892First holderEdwin G. EastmanSalary$141,390 (2022)Websitedoj.nh.gov Attorney general for the U.S. state of New Hampshire The Attorney General of New Hampshire is a constitutional offi…

Ini adalah nama Batak Pakpak, marganya adalah Solin.Mutsyuhito Solin Wakil Bupati Pakpak Bharat ke-3PetahanaMulai menjabat 26 Februari 2021PresidenJoko WidodoGubernurEdy Rahmayadi PendahuluMaju Ilyas PadangPenggantiPetahanaBupatiFranc Bernhard Tumanggor Informasi pribadiLahir6 Oktober 1958 (umur 65)Sidikalang, Sumatera UtaraKebangsaanIndonesiaSuami/istriProf. Dr. Hj. Sri Minda Murni, M.S.Anak1. Syafiq Anshori M. Solin, M.Hum 2. Nida Wafiqah M. Solin, M.Si 3. Thareq Muhammad M. Solin…

Kejuaraan Eropa U-21 UEFA 1998Campionatul European de Fotbal sub 21 UEFA 1998Informasi turnamenTuan rumah RumaniaJadwalpenyelenggaraan23–31 MeiJumlahtim peserta8 (dari 1 konfederasi)Tempatpenyelenggaraan3 (di 1 kota)Hasil turnamenJuara Spanyol (gelar ke-2)Tempat kedua YunaniTempat ketiga NorwegiaTempat keempat BelandaStatistik turnamenJumlahpertandingan12Jumlah gol22 (1,83 per pertandingan)Pemain terbaik Francesc ArnauPencetak golterbanyak Steffen Iverse…

Romanian footballer and manager Coloman Braun-Bogdan Personal informationDate of birth (1905-10-13)13 October 1905Place of birth Arad, Austria-HungaryDate of death 15 March 1983(1983-03-15) (aged 77)Position(s) MidfielderSenior career*Years Team Apps (Gls)1920–1932 AMEF Arad 1932–1934 Racing Club Calais 1934–1935 Juventus București 12 (0)1936–1938 Juventus București 30 (0)Total 42 (0)Managerial career1936–1937 Sportul Studențesc București1937–1938 Juventus București1940 Juv…

2002 2012 Élections législatives de 2007 dans la Drôme 4 sièges de députés à l'Assemblée nationale 10 et 17 juin 2007 Corps électoral et résultats Inscrits 339 250 Votants au 1er tour 208 447 61,44 % 5,3 Votes exprimés au 1er tour 205 216 Votants au 2d tour 209 499 61,75 % Votes exprimés au 2d tour 202 626 Majorité présidentielle Liste Union pour un mouvement populaireDivers droite (Maj. prés.)Divers droiteMouvement pour l…

Primeira Divisão 1962-1963 Competizione Primeira Divisão Sport Calcio Edizione 25ª Organizzatore FPF Date dal 1962al 1963 Luogo Portogallo Partecipanti 14 Cronologia della competizione 1961-62 1963-64 Manuale L'edizione 1962-63 della Primeira Divisão vide la vittoria finale del Benfica. Capocannoniere del torneo fu José Augusto Torres (Benfica), con 26 reti. Indice 1 Classifica finale 1.1 Verdetti 1.2 Record 2 Risultati 3 Voci correlate 4 Collegamenti esterni Classifica finale…
Vaishnava Hindu text Avyakta UpanishadThere was nothing, then appeared light, then universe states Avyakta UpanishadDevanagariअव्यक्तोपनिषत्IASTAvyaktaTitle meansNon-manifest, universal SpiritDateparts before 7th century CE[1]TypeVaishnavismLinked VedaSama VedaChapters7Verses21[1]PhilosophySamkhya, Yoga, Vedanta Part of a series onVaishnavism Supreme deity Vishnu / Krishna / Rama Important deities Dashavatara Matsya Kurma Varaha Narasimha Vamana Parasu…

Into the FirePromotional film poster for Into the Fire.SutradaraMichael PhelanProduserDavid CrockettMichael PhelanBryan ThomasLisa YeskoDitulis olehMichael PhelanPemeranSean Patrick FlaneryMelina KanakaredesJoBeth WilliamsPablo SchreiberPenata musikMatt AnthonyStephen O'ReillySinematograferChris NoorPenyuntingShawna CallahanDistributorSilent Thunder EntertainmentTanggal rilis16 Februari 2007 (Argentina)BahasaInggrisIMDbInformasi di IMDb Into the Fire adalah salah satu film Amerika Serikat …

Light rail station in Aurora, Colorado 2nd Avenue & Abilene R 2nd Avenue & Abilene station platform in February 2017General informationOther names2nd Ave•AbileneLocation14051 East Ellsworth AvenueAurora, ColoradoCoordinates39°43′10.0″N 104°49′32.4″W / 39.719444°N 104.825667°W / 39.719444; -104.825667Owned byRegional Transportation DistrictLine(s)I-225 Corridor[1]Platforms2 side platformsTracks2Connections RTD Bus: 6Construction…










![{\displaystyle {\begin{aligned}&\forall x\,\forall y\,\forall z\,\forall p_{1}\ldots \forall p_{n}[\varphi (x,y,p_{1},\ldots ,p_{n})\wedge \varphi (x,z,p_{1},\ldots ,p_{n})\implies y=z]\implies \\&\forall A\,\exists B\,\forall y(y\in B\iff \exists x(x\in A\wedge \varphi (x,y,p_{1},\ldots ,p_{n})))\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1d1fd930959be3d579d2dc3e93ddd60bf8114815)










![{\displaystyle \exists D\forall C\,([C\in D]\iff [P(C)\land \exists E\,(C\in E)])\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9618691c77d4976bb428f92baf1c4fc192896289)
![{\displaystyle \forall D\forall A\,(\exists E\,[A\in E]\implies \exists B\,[\exists E\,(B\in E)\land \forall C\,(C\in B\iff [C\in A\land C\in D])])\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d7a213bab05ab2f6985caa5d1637495cd12eba24)
![{\displaystyle \forall A\forall B\,([\exists E\,(A\in E)\land \forall C\,(C\in B\implies C\in A)]\implies \exists E\,[B\in E])\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/38ea7cc02153e6cdc550833f6b7fdc0dcda35fce)

