Transfinite induction
|
Read other articles:

Shiva is a Hindu deity worshipped by Shaivaites in India as well as Pakistan as the destroyer of ignorance spread all across the universe. As one of the three main gods in the Hindu pantheon, there are temples dedicated to his worship in India and Pakistan as well (and abroad). The most prominent of these is the Jyotirlinga temples and Mellacheruvu Swayabhu Shambhulingeshwara Swami. In Shaivism, Shiva is the god of all and is described as worshipped by all, including Devas (gods) like Brahma, Vi…

Untuk kegunaan lain, lihat Ranah 3 Warna. Ranah 3 WarnaPosterSutradaraGuntur SoeharjantoProduserWidya Wardhani IchramSkenarioAlim SudioBerdasarkanRanah 3 Warnaoleh Ahmad FuadiPemeran Arbani Yasiz Amanda Rawles Teuku Rassya Lukman Sardi Maudy Koesnaedi Tanta Ginting Asri Welas Penata musikRicky LionardiSinematograferFahmi J. SaadPenyuntingLilik SubagyoPerusahaanproduksiMNC PicturesTanggal rilis 18 November 2021 (2021-11-18) (JFW) 30 Juni 2022 (2022-06-30) (Indonesia) Duras…
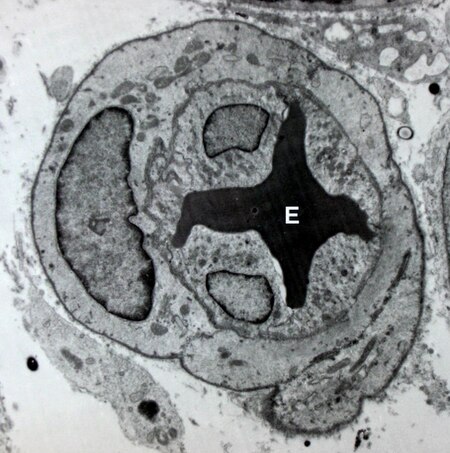
Tubular structure of the circulatory system which transports blood For other uses, see Blood vessel (disambiguation). Blood vesselSimple diagram of the human circulatory systemDetailsSystemCirculatory systemIdentifiersLatinvas sanguineumMeSHD001808TA98A12.0.00.001TA23895FMA63183Anatomical terminology[edit on Wikidata] Blood vessels are the components of the circulatory system that transport blood throughout the human body.[1] These vessels transport blood cells, nutrients, and oxygen…

Hak properti wanita adalah hak hukum bagi wanita untuk mendapatkan, memiliki, menjual, mentransfer properti, mengumpulkan dan menyimpan sewa, memiliki pendapatan, membuat kontrak, dan membawa perangkat hukum,[1] yang berdasarkan hukum umum Inggris (English common law). Selama periode modern awal, hak properti bagi wanita tersebut tidak diberikan.[2] Ratu Victoria di dalam kereta beserta rakyat Dublin di Grafton street Pada Victorian Era (masa pemerintahan Ratu Victoria) terdapat …

Komando Daerah Militer XVII/CenderawasihLambang Kodam XVII/CenderawasihDibentuk17 Mei 1963Negara IndonesiaTipe unitKomando Daerah MiliterBagian dariTNI Angkatan DaratMarkasJayapura, PapuaMotoKsatria Pelindung RakyatBaret HIJAU HimneMars CenderawasihSitus webkodam17cenderawasih-tniad.mil.idTokohPanglimaMayor Jenderal TNI Izak PangemananKepala StafBrigadir Jenderal TNI HariyantoInspekturBrigadir Jenderal TNI MukhlisKepala Kelompok Staf AhliBrigadir Jenderal TNI Achmad Fauzi Komando Daera…

CataloniaNickname(s)El XV de la ginesta (the XV of the Broom)EmblemSpanish broom flowerUnionCatalan Rugby Federation (Catalan: Federació Catalana de Rugbi)Head coachÁlvaro HompaneraHome stadiumCamp de la Foixarda First colours Second colours First international Catalonia 5 – 5 Italy(Camp de Les Corts; 14 April 1934)Biggest win Catalonia 66 – 6 Andorra(Sant Boi; 25 March 1995)Biggest defeat Catalonia 15 – 67 Russia(L'Hospitalet; 24 March 1998)Websitewww.rugby.cat The Cat…

У слова «Лютый» есть и другие значения; см. Лютый. Иоан Водэ Лютыймолд. Ион Водэ (Арманул) господарь Молдавского княжества Рождение 1521(1521) Смерть 14 июля 1574(1574-07-14)Roșcani[d], Băneasa[d], Covurlui County[d], Галац, Румыния Род Мушаты (Мушатины) Отец Стефан IV[1] Дети Ștefan Surdul[d] Отношение к рел�…

此條目介紹的是拉丁字母中的第2个字母。关于其他用法,请见「B (消歧义)」。 提示:此条目页的主题不是希腊字母Β、西里尔字母В、Б、Ъ、Ь或德语字母ẞ、ß。 BB b(见下)用法書寫系統拉丁字母英文字母ISO基本拉丁字母(英语:ISO basic Latin alphabet)类型全音素文字相关所属語言拉丁语读音方法 [b][p][ɓ](适应变体)Unicode编码U+0042, U+0062字母顺位2数值 2歷史發展…

Artikel ini bukan mengenai Aliyah. Halaman ini berisi artikel tentang sang penyanyi. Untuk album miliknya, lihat Aaliyah (album). AaliyahAaliyah pada tahun 2000LahirAaliyah Dana Haughton(1979-01-16)16 Januari 1979New York City, Amerika SerikatMeninggal25 Agustus 2001(2001-08-25) (umur 22)Marsh Harbour, Kepulauan Abaco, BahamaSebab meninggalKecelakaan pesawatMakamPemakaman FerncliffHartsdale, New York, A.S.Nama lainBabygirlPekerjaan Penyanyi aktris model penari Tahun aktif1989…

Netherlands electricity generation by source Despite the historic usage of wind power to drain water and grind grain, the Netherlands today lags 21 of the 26 other member states of the European Union in the consumption of energy from renewable sources. In 2022, the Netherlands consumed just 15% of its total energy from renewables.[1] According to statistics published by Eurostat, it was the last among the EU countries in the shift away from global warming-inducing energy sources.[2&#…

Pierre Ier du Brésil et IV de Portugal. Le Dia do Fico (en français : jour du je reste), arriva le 9 janvier 1822 quand le futur Pierre Ier du Brésil refusa les ordres des Cortes portugaises qui exigeaient son retour à Lisbonne et resta au Brésil. Contexte et déroulement Vers 1821, quand les Cortes portugaises commencèrent à penser à refaire du Brésil une colonie, les libéraux radicaux s'unirent au Parti brésilien pour maintenir l'autonomie du Brésil. Les Cortes envoyèrent alo…

Peta jalur kereta api Trans-Siberia berwarna merah Jalur kereta api Trans-Siberia (Trans-Siberian Railway, Транссибирская магистраль, Транссиб dalam bahasa Rusia, atau Transsibirskaya magistral', Transsib) adalah jaringan kereta api yang menghubungkan Moskow dan Eropa Rusia dengan provinsi-provinsi Timur Jauh Rusia, Mongolia, Tiongkok dan Laut Jepang.[1] Dengan panjang 9.289 km (5.772 mil),[2] jalur ini merupakan jalur kereta terpanjang d…

Freestyle skiingat the XXIII Olympic Winter Games Pictograms from top, left to right: Aerials, Halfpipe, Moguls, Ski Cross, and Slopestyle.VenueBokwang Phoenix ParkDates9–23 FebruaryNo. of events10 (5 men, 5 women)Competitors268 from 27 nations← 20142022 → Freestyle skiing at the2018 Winter OlympicsQualification AerialsmenwomenHalfpipemenwomenMogulsmenwomenSki crossmenwomenSlopestylemenwomenvte Freestyle skiing at the 2018 Winter Olympics was held at the Bokwang…

Wakil Bupati SikkaPetahanaRomanus Wogasejak 20 September 2018Masa jabatan5 tahunDibentuk2003Pejabat pertamaDrs. Pieter R. Lobo, M.Si.Situs webwww.sikkakab.go.id/welcome Berikut ini adalah daftar Wakil Bupati Sikka dari masa ke masa. No Potret Wakil Bupati Mulai Jabatan Akhir Jabatan Prd. Ket. Bupati 1 Drs.Yoseph Ansar Rera 31 Mei 2003 31 Mei 2008 1 Drs.Alexander Longginus 2 dr.Wera DamianusM.M. 31 Mei 2008 31 Mei 2013 2 [1] Drs.Sosimus Mitang Jabatan kosong 31 Mei 2013 6 Juli…

الدوري السعودي الممتاز تفاصيل الموسم 1989–1990 النسخة 14 البلد السعودية البطل الهلال (سادس لقب) الهابطون النهضةالرائد عدد المشاركين 12 الهداف سامي الجابر (16 هدف) 1988–89 1990–91 تعديل مصدري - تعديل الدوري السعودي الممتاز 1989–1990 هي النسخة الرابعة عشر من الدوري السعودي الم…

شمبلين الإحداثيات 45°34′25″N 74°39′28″W / 45.573611111111°N 74.657777777778°W / 45.573611111111; -74.657777777778 [1] [2] تقسيم إداري البلد كندا[3] معلومات أخرى K0B رمز جيونيمز 5919683 الموقع الرسمي الموقع الرسمي تعديل مصدري - تعديل شمبلين، أونتاريو (بالإنجليزية…

Art installation in Germany Tiger and Turtle – Magic Mountain Tiger and Turtle – Magic Mountain is an art installation and landmark in Duisburg, Germany, built in 2011.[1][2] It was designed by Ulrich Genth and Heike Mutter. It resembles a roller coaster, but it is a walkway with stairs. Its vertical loop continues the walkway and stairs, but it is unwalkable and is blocked off. In 2013, Tiger and Turtle – Magic Mountain was ranked as #6 on HuffPost's list of Most Extreme S…

Phenomenon of US political rhetoric after WWII This article is about the events during the cold war. For general information about the phenomenon, see Red Scare. American anti-communist propaganda of the 1950s, specifically addressing the entertainment industry McCarthyism, also known as the Second Red Scare, was the political repression and persecution of left-wing individuals and a campaign spreading fear of alleged communist and Soviet influence on American institutions and of Soviet espionag…

Spanish guitarist and composer Gaspar SanzGaspar Sanz. A detail from the dedication page of Instrucción de música may be an image of SanzBornFrancisco Bartolomé Sanz Celmabaptized April 4, 1640 (birth date unknown)Calanda, Bajo Aragón, SpainDied1710 (aged 70)Madrid, SpainOccupation(s)composer and priest Francisco Bartolomé Sanz Celma (April 4, 1640 (baptized) – 1710), better known as Gaspar Sanz, was a Spanish composer, guitarist, and priest born to a wealthy family in Calanda in the coma…

此條目可参照英語維基百科相應條目来扩充。若您熟悉来源语言和主题,请协助参考外语维基百科扩充条目。请勿直接提交机械翻译,也不要翻译不可靠、低品质内容。依版权协议,译文需在编辑摘要注明来源,或于讨论页顶部标记{{Translated page}}标签。 此生者传记条目需要补充更多可供查證的来源。 (2013年3月23日)请协助補充可靠来源,无法查证的在世人物内容将被立即移除�…





















