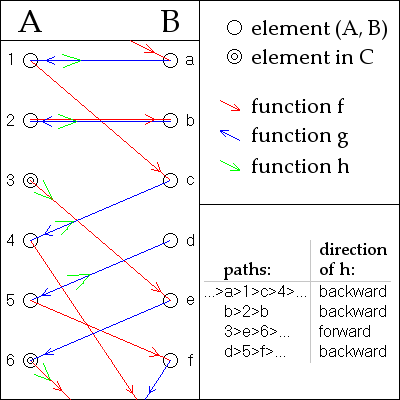
Schröder–Bernstein theorem
|

Within the Indo-Greek Kingdom there were over 30 kings, often in competition on different territories. Many of them are only known through their coins. Many of the dates, territories, and relationships between Indo-Greek kings are tentative and essentially based on numismatic analysis (find places, overstrikes, monograms, metallurgy, styles), a few Classical writings, and Indian writings and epigraphic evidence. The following list of kings, dates and territories after the reign of Demetrius is d…

Komando Distrik Militer 1014Lambang Kodam XII TanjungpuraNegara IndonesiaAliansiKorem 102/Panju PanjungCabangTNI Angkatan DaratTipe unitKodimPeranSatuan TeritorialBagian dariKodam XII/TanjungpuraMakodimPangkalan Bun, Kalimantan TengahJulukanKodim 1014/PbnPelindungTentara Nasional IndonesiaBaret H I J A U TokohKomandanLetkol Arh. Drajat Tri PutroKepala StafMayor Komando Distrik Militer 1014/Pangkalan Bun atau Kodim 1014/Pbn merupakan salah satu Kodim di jajaran Korem 102/Panju Panj…

Uang logam Antigonus (40-37 SM) Uang logam Hashmonayim (bahasa Inggris: Hasmonean coinage) adalah uang-uang dari logam yang dicetak oleh raja-raja Hashmonayim. Yang diketemukan hanya uang-uang dari perunggu dalam berbagai denominasi; yang terkecil bernilai satu prutah atau setengah prutah. Dua uang denari perak Romawi juga dikaitkan dengan zaman Hashmonayim; salah satunya memuat tulisan BACCIUS JUDAEAS; arti pastinya belum jelas. Keduanya memuat gambar seseorang yang diduga adalah Yehuda Ari…

Pre-Columbian Mesoamerican site in the highlands of Guatemala IximcheLocation within GuatemalaLocationTecpán GuatemalaRegionChimaltenango Department, GuatemalaCoordinates14°44′8.88″N 90°59′46.32″W / 14.7358000°N 90.9962000°W / 14.7358000; -90.9962000HistoryFounded1470Abandoned1524PeriodsLate PostclassicCulturesKaqchikel MayaEventsConquered by:SpainSite notesArchaeologistsJorge Guillemín Map of the Guatemalan highlands in the Postclassic Period Iximcheʼ…

Untuk band, lihat Madison Avenue (band). Madison Avenue, menghadap ke utara dari 40th Street Madison Avenue adalah sebuah jalan utara-selatan di borough Manhattan di New York City, Amerika Serikat yang membawa lalu lintas satu arah ke utara. Jalan ini membentang dari Madison Square (di 23rd Street) ke Jembatan Madison Avenue di 138th Street. Sepanjang bentangan ini, jalan ini melintasi Midtown, Upper East Side (termasuk Carnegie Hill), Spanish Harlem, dan Harlem. Jalan ini dinamai sesuai Madison…

Museum Gletser Norwegia Museum Gletser Norwegia (bahasa Norwegia: Norsk Bremuseum) adalah sebuah museum di Fjærland, Sogn og Fjordane, Norwegia.[1] Bangunan tersebut dirancang oleh arsitek Sverre Fehn. Referensi ^ Anne-Sofie Hjemdahl. Norsk Bremuseum – Bresenteret i Fjærland. Store norske leksikon. Diakses tanggal September 1, 2017. Pranala luar Norsk Bremuseum Website Climate Exhibition at Norwegian Glacier Museum Wikimedia Commons memiliki media mengenai Norwegian Glacier…

Artikel ini perlu dikembangkan agar dapat memenuhi kriteria sebagai entri Wikipedia.Bantulah untuk mengembangkan artikel ini. Jika tidak dikembangkan, artikel ini akan dihapus. State of ParáState BenderaLambang kebesaranLocation of State of Pará in BrazilCountry BrazilCapital and Largest CityBelémPemerintahan • GovernorSimão Jatene • Vice GovernorHelenilson PontesLuas • Total1.247.689,5 km2 (4,817,356 sq mi)Peringkat2ndPopulasi (20…

Putri AnitaPutri Anita dari Oranye-Nassau, van Vollenhoven-van EijkPutri Anita (2013)Kelahiran27 Oktober 1969 (umur 54)Neuchâtel, SwissWangsaWangsa Oranye-NassauAyahLeonardus Antonius van EijkIbuJ.C.M. van Eijk-SteensPasanganPangeran Pieter-ChristiaanAnakEmma van VolenhovenPieter van Vollenhoven Putri Anita Theodora dari Oranye-Nassau, van Vollenhoven-van Eijk (nama lazim Anita Theodora van Vollenhoven-van Eijk, lahir 27 Oktober 1969), adalah istri Pangeran Pieter-Christiaan dari Oranye-Na…

Ban Kong-EkBan Kong-EkLokasi di LaosKoordinat: 14°36′N 107°1′E / 14.600°N 107.017°E / 14.600; 107.017Koordinat: 14°36′N 107°1′E / 14.600°N 107.017°E / 14.600; 107.017Negara LaosProvinsiProvinsi AttopuZona waktuUTC + 7 Ban Kong-Ek adalah sebuah desa di Distrik Phouvong, Provinsi Attopu, Laos tenggara.[1] Referensi ^ Maplandia world gazetteer lbs Distrik Phouvong, provinsi Attopu, LaosKota-kota dan desa-desa Ban Arapruich Ban …

Untuk periodikal abad ke-19, lihat The Galaxy (majalah). Sampul David Stone untuk keluaran pertama Galaxy Galaxy Science Fiction adalah sebuah majalah fiksi ilmiah Amerika, yang diterbitkan dari 1950 sampai 1980. Ini didirikan oleh perusahaan Prancis-Italia, World Editions, yang berniat masuk pasar Amerika. World Editions disewa saat penyunting H. L. Gold, yang cepat membuat Galaxy menjadi majalah fiksi ilmiah utama pada masa itu, berfokus pada cerita tentang masalah sosial ketimbang teknologi. …

Dalam nama Tionghoa ini, nama keluarganya adalah Chen. Untuk orang lain dengan nama yang sama, lihat Chen Dong. Chen DongLahir12 Desember 1978 (umur 45)Luoyang, HenanStatusAktifKebangsaanTiongkokPekerjaanPilot tempurKarier luar angkasaAntariksawan Badan Antariksa Nasional TiongkokPekerjaan saat iniAntariksawanPangkatLetkol Pasukan Pendukung Strategis Tentara Pembebasan RakyatWaktu di luar angkasa32 hari 06 jam 25 menit [1]SeleksiKelompok Tiongkok 2MisiShenzhou 11 Chen Dong (Hanzi se…

Kereta Hefei-WuhanJalur Kereta Hewu di County Jinzhai, AnhuiIkhtisarNama lainJalur HewuNama asli合武铁路JenisKelas IStatusBeroperasiLokasiAnhui dan Hubei, TiongkokTerminus(Rawas)(Rawas)Stasiun13OperasiDibuka31 Desember 2008OperatorKereta api kecepatan tinggi TiongkokData teknisPanjang lintas359 km (223 mi)Lebar sepur1.435 mm (4 ft 8+1⁄2 in) sepur standarElektrifikasi25 kV ACKecepatan operasi250 km/h (160 mph) Kereta Hefei-Wuhan atau Jalur Kereta …

Anna of Tyrol by Alessandro Abondio, 1618 The funeral effigy (without clothes) of Elizabeth of York, mother of King Henry VIII, 1503, Westminster Abbey The Beatles at Madame Tussauds London Cecilia Cheung at Madame Tussauds Hong Kong A wax sculpture is a depiction made using a waxy substance. Often these are effigies, usually of a notable individual, but there are also death masks and scenes with many figures, mostly in relief. The properties of beeswax make it an excellent medium for preparing …

Direktorat Topografi Angkatan DaratLambang Direktorat Topografi Angkatan DaratDibentuk26 April 1946Negara IndonesiaCabangTNI Angkatan DaratBagian dariTentara Nasional IndonesiaMotoLhikita Bhutala Yudha KaryaTokohDirekturBrigadir Jenderal TNI Ir. Adik Sugianto Direktorat Topgrafi Angkatan Darat atau Dittopad adalah adalah Badan Pelaksana Pusat di tingkat Mabes AD yang berkedudukan langsung dibawah KASAD. Dittopad bertugas pokok menyelenggarakan pembinaan kecabangan, pembinaan personel dan fu…

Sebuah casing bom alumunium Mark 4N.[1] Bom nuklir Mark 4 adalah sebuah desain bom nuklir Amerika yang mulai dibuat pada 1949 dan dipakai sampai 1953. Mark 4 berdasarkan pada desain Mark 3 Fat Man pada masa sebelumnya, yang diapaki dalam uji coba Trinity dan serangan bom Nagasaki. Referensi ^ Hansen, Charles (2007) [1995]. Swords of Armaggedon:Volume V. Sunnyvale, CA: Chukelea Productions. hlm. V180, V179. ISBN 978-0-9791915-5-8. Pranala luar Allbombs.html list of all U.S…

Untuk keuskupan bernama sama dalam Gereja Irlandia, lihat Keuskupan Clogher (Gereja Irlandia). Keuskupan ClogherDioecesis ClogheriensisDeoise ChlochairKatolik Katedral St Macartan, MonaghanLokasiNegara Irlandia Utara Republik IrlandiaProvinsi gerejawiProvinsi ArmaghStatistikLuas3.456 sq mi (8.950 km2)Populasi- Total- Katolik(per 2016)11370088,400 (77.7%)InformasiDenominasiKatolik RomaRitusRitus LatinKatedralKatedral St Macartan, MonaghanPelindungSt Ma…

Charles Savarin Presiden Dominika ke-8Masa jabatan2 Oktober 2013 – 2 Oktober 2023Perdana MenteriRoosevelt Skerrit PendahuluEliud WilliamsPenggantiSylvanie Burton Informasi pribadiLahir2 Oktober 1943 (umur 80)Portsmouth, Kepulauan Leeward InggrisSuami/istriClara Josephine SavarinAlma materRuskin CollegeSunting kotak info • L • B Charles Angelo Savarin (lahir 2 Oktober 1943) adalah seorang politikus dari Dominika yang telah menjadi Presiden Dominika dari 2013 hingga 2…

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada November 2022. Bellan RoosRoos pada 1927Lahir(1901-05-25)25 Mei 1901Nynäshamn, SwediaMeninggal8 April 1990(1990-04-08) (umur 88)Stockholm, SwediaPekerjaanPemeranTahun aktif1933-1979 Bellan Roos (25 Mei 1901 – 8 April 1990) adalah seorang peme…

Artikel ini membutuhkan rujukan tambahan agar kualitasnya dapat dipastikan. Mohon bantu kami mengembangkan artikel ini dengan cara menambahkan rujukan ke sumber tepercaya. Pernyataan tak bersumber bisa saja dipertentangkan dan dihapus.Cari sumber: Kuskus tanah – berita · surat kabar · buku · cendekiawan · JSTOR (Januari 2024) Artikel ini perlu diwikifikasi agar memenuhi standar kualitas Wikipedia. Anda dapat memberikan bantuan berupa penambahan pranala da…

System of flowering plant classification The Cronquist system is a taxonomic classification system of flowering plants. It was developed by Arthur Cronquist in a series of monographs and texts, including The Evolution and Classification of Flowering Plants (1968; 2nd edition, 1988) and An Integrated System of Classification of Flowering Plants (1981) (see Bibliography). Cronquist's system places flowering plants into two broad classes, Magnoliopsida (dicotyledons) and Liliopsida (monocotyledons)…





![{\displaystyle [0,1]\to [0,1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/17a36f8747ab3ee636af08662bf42afaccc712e6)

![{\displaystyle f:[0,1]\to [0,1)\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c64a1a0a61a5f6d457d4e652d05432f6338cf638)

![{\displaystyle g:[0,1)\to [0,1]\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2e2914572daa48f17ee09e5095f72455c62dcefe)


![{\displaystyle \;h(x)={\begin{cases}{\frac {x}{2}},&\mathrm {for} \ x\in C\\x,&\mathrm {for} \ x\in [0,1]\setminus C\end{cases}}\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4ff1a29581709e0207057e542c46803fdae2cc4c)




















