Higher category theory
|
Read other articles:

Guildford — Kota — Searah jarum jam dari kiri: Stasiun kereta api Guildford, the High Street, Katedral Guildford dengan pemukiman warga, the Guildhall, and the Electric Theatre di samping Sungai Wey. Population 77,057 (2011) Ref. grid OS SU9949 - London 27 mil (43 km) NE District Guildford County shire Surrey Wilayah Negara konstituen Inggris Negara berdaulat Britania Raya Distrik kode pos …

Artikel ini bukan mengenai Anteraja. Untuk mesin, lihat Antareja (mesin). AntarejaWayang Antareja gaya Surakarta.Tokoh pewayangan JawaJenis kelaminlaki-lakiKeistimewaankulit kebal; mampu hidup dan berjalan di dalam tanah.KeluargaWerkudara (ayah)Nagini (ibu) Anantaraja, atau yang lebih sering disingkat Antareja, adalah salah satu tokoh pewayangan Jawa. Antareja sering dikisahkan terlibat dengan tokoh-tokoh wiracarita Mahabharata, tetapi nama Antareja tidak terdapat dalam naskah Mahabharata karya …

Anna AtkinsAnna Atkins pada tahun 1861Lahir(1799-03-16)16 Maret 1799Tonbridge, Kent, InggrisMeninggal9 Juni 1871(1871-06-09) (umur 72)Halstead Place, Sevenoaks, Kent, InggrisKebangsaanInggrisDikenal atasFotografer botani pertama, pembuat buku Photographs of British Algae: Cyanotype Impressions (buku pertama dilengkapi dengan ilustrasi gambar foto)Karier ilmiahBidangBotani, FotografiTerinspirasiJohn George ChildrenWilliam Henry Fox TalbotJohn Frederick William Herschel Anna Atkins (Nama lahi…

Hayu Dyah PatriaBerkas:Hayu dyah.jpgLahir27 Januari 1981 (umur 43)Gresik, Jawa TimurKebangsaan IndonesiaPekerjaanMemanfaatkan tumbuhan liar sebagai pangan.Dikenal atasMengembangkan gizi di tanaman liar, mendapat penghargaan Satu Award. Hayu Dyah Patria (lahir 27 Januari 1981) adalah seorang pemberdaya makanan yang mendapat penghargaan Satu Award. Inisiatif Latar belakang Ia memanfaatkan tanaman liar untuk memenuhi gizi masyarakat. Bahkan, ia berencana untuk mengadakan festival makanan dari …
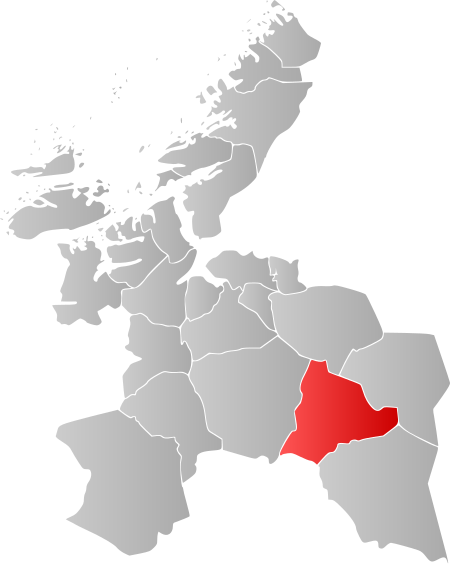
Holtålen ialah sebuah kotamadya di provinsi Sør-Trøndelag, Norwegia. Lambang Lambang Holtålen Lambangnya berasal dari masa modern, yang menampilkan burung belibis (Lagopus; 1988). Geografi Peta lokasi Lembah Gauldalen dengan sungainya Gaula berasal dari daerah pegunungan sekitar kota pertambangan Roeros 35 selatan Ålen, dan didaftarkan di Warisan Dunia. Gaula mengalir ke muara di Melhus dekat Trondheim. Desa Aalen, pusat administratif kotamadya ini, ditemukan di mana sebuah lembah yang dala…

The Little GypsySutradaraOscar ApfelProduserWilliam FoxDitulis olehMary MurilloPemeranDorothy BernardSinematograferAlfredo GandolfiDistributorFox Film CorporationTanggal rilis10 Oktober 1915Durasi50 menitNegaraAmerika SerikatBahasaBisu The Little Gypsy adalah sebuah film drama bisu tahun 1915 yang hilang[1] garapan Oscar Apfel dan menampilkan Dorothy Bernard. Film tersebut diproduksi oleh William Fox dan dirilis melalui Fox Film Corporation.[2][3] Pemeran Dorothy Bernard …

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (سبتمبر 2019) هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (…

City in Wisconsin, United StatesRichland CenterCityRichland Center's historic downtown, viewed from Court and Main StreetLocation of Richland Center in Richland County, WisconsinRichland CenterShow map of WisconsinRichland CenterShow map of the United StatesCoordinates: 43°20′16″N 90°23′5″W / 43.33778°N 90.38472°W / 43.33778; -90.38472Country United StatesState WisconsinCountyRichlandArea[1] • Total4.77 sq mi (12.41 …

Dilan Yeşilgöz-Zegerius Dilan Yeşilgöz-Zegerius (lahir 18 Juni 1977) adalah seorang politikus Belanda yang lahir di Ankara, Turki. Ia menjabat Menteri Kehakiman dan Keamanan sejak 10 Januari 2022. Dia adalah anggota Partai Rakyat untuk Kebebasan dan Demokrasi (VVD).[1] Referensi D. (Dilan) Yesilgöz-Zegerius, Parlement.com ^ Rekor Baru di Belanda, 14 Perempuan Akan Duduki Posisi Menteri. Tempo. lbs Anggota Tweede Kamer (2023–)sejak 6 Desember 2023Partai untuk Kebebasan (PVV �…

Об экономическом термине см. Первородный грех (экономика). ХристианствоБиблия Ветхий Завет Новый Завет Евангелие Десять заповедей Нагорная проповедь Апокрифы Бог, Троица Бог Отец Иисус Христос Святой Дух История христианства Апостолы Хронология христианства Ранне…

Indonesian theatre This article's edit history is not complete. Some of the article text's edit history exists at different locations due to copying and pasting between articles. This may be a violation of the CC BY-SA and/or GFDL if proper attribution was not made in an edit summary or on the talk page. Please see Wikipedia:Merge and Wikipedia:Splitting for details of how to correctly attribute using links in the edit summaries. You can also read the copying within Wikipedia guideline for an ov…

Castle in Denmark Krengerup Krengerup is a Neoclassical manor house located near Glamsbjerg some 15 km (9.3 mi) northeast of Assens on the Danish island of Funen. History and architecture The first references to Krengerup are from 1514 but the estate seems to be older. Since 1770, it has belonged to the Rantzau family. It was the principal property on a large estate which included Søholm and Brahesholm. In 1590, Gabriel Knudsen Akeleye built a thatched half-timbered house on the site …

イスラームにおける結婚(イスラームにおけるけっこん)とは、二者の間で行われる法的な契約である。新郎新婦は自身の自由な意思で結婚に同意する。口頭または紙面での規則に従った拘束的な契約は、イスラームの結婚で不可欠だと考えられており、新郎と新婦の権利と責任の概要を示している[1]。イスラームにおける離婚は様々な形をとることができ、個人的…

Adelantado(penguasa militer)Pedro de Valdivia Gubernur Kerajaan ke-1 di ChiliMasa jabatan1540–1547Penguasa monarkiCharles I dari SpanyolPendahuluTidak adaPenggantiFrancisco de VillagraMasa jabatan1549–1553Penguasa monarkiCharles I dari SpanyolPerdana MenteriPedro de la GascaPendahuluFrancisco de VillagraPenggantiFrancisco de Villagra Informasi pribadiLahirk. 1500Castuera de la Serena, Extremadura, SpanyolMeninggal25 Desember 1553(1553-12-25) (umur 53) invalid month invalid dayTu…

Dam in Riverina, New South WalesHume DamAerial view of Hume Dam and spillway, 2012Location of the Hume Dam inNew South WalesCountryAustraliaLocationRiverina, New South WalesCoordinates36°06′30″S 147°01′52″E / 36.10833°S 147.03111°E / -36.10833; 147.03111PurposeFlood mitigation, hydro-power, irrigation, water supply and conservationStatusOperationalConstruction began1919 (1919)Opening date1936 (1936)Construction costA£2.1 million&…

Voluntary organisation and registered charity Leeds Civic TrustShop and offices at 17–19 Wharf StreetFormation25 October 1965; 58 years ago (25 October 1965)TypeRegistered charityRegistration no.2742348[1]Legal statusCompany limited by guarantee[1]PurposeCivic societyHeadquarters17–19 Wharf StreetLocationLeeds LS2 7EQDirectorMartin HamiltonChair of TrusteesJane TaylorPublicationOutlookStaff 3Websiteleedscivictrust.org.uk Leeds Civic Trust is a voluntary orga…

Thai media mogul (born 1947) Sondhi Limthongkulสนธิ ลิ้มทองกุลSondhi LimthongkulBorn (1947-11-07) 7 November 1947 (age 76)Sukhothai, ThailandAlma materUtah State UniversityUCLAOccupationsPublisherauthoractivistYears active1973–20162019–presentSpouseChanthip LimthongkulChildrenJittanart Limthongkul Sondhi Limthongkul (Thai: สนธิ ลิ้มทองกุล; RTGS: Sonthi Limthongkun; Chinese: 林明達; pinyin: Lín Míngdá, born 7…

Cet article concerne la série télévisée. Pour son adaptation au cinéma, voir L'Agence tous risques (film). Pour les articles homonymes, voir ATR. Ne doit pas être confondu avec Pour l'amour du risque. L'Agence tous risques Logo original de la série. Données clés Titre original The A-Team Genre Série d'action Création Frank LupoStephen J. Cannell Acteurs principaux George PeppardDirk BenedictDwight SchultzMister T Musique Mike PostPete Carpenter (en) Pays d'origine États-Unis…

Women's collegiate basketball program Colgate Raiders women's basketball 2023–24 Colgate Raiders women's basketball team UniversityColgate UniversityHead coachGaniyat Adeduntan (1st season)ConferencePatriotLocationHamilton, New YorkArenaCotterell Court (Capacity: 1,750)NicknameRaidersColorsMaroon and white[1] Uniforms Home Away NCAA tournament appearances2004Conference tournament champions2004 The Colgate Raiders women’s basketball team is the college baske…

Unique headings used for bibliographic information For information on authority control usage within Wikipedia, see Help:Authority control. In information science, authority control is a process that organizes information, for example in library catalogs,[1][2][3] by using a single, distinct spelling of a name (heading) or an (generally alphanumeric) identifier for each topic or concept. The word authority in authority control derives from the idea that the names of peopl…
