Groupe de frise
|
Read other articles:

California Hall of Fame dengan Gubernur dan istrinya. California Hall of Fame yang didirikan oleh Museum Sejarah, Wanita dan Seni California adalah penghargaan untuk menghargai orang dan keluarga legendaris di California. Pada tanggal 6 Desember 2006, orang seperti: Ronald Reagan, César Chávez, Walt Disney, Amelia Earhart, Clint Eastwood, Frank Gehry, David D. Ho, M.D., Billie Jean King, John Muir, Sally K. Ride, Ph.D., Alice Walker dan the Hearst dan Packard Families dimasukan kedalam Califor…

Edward si Pangeran HitamPangeran Wales, Pangeran Aquitaine,Adipati Cornwall, Earl of ChesterEdward, Pangeran WalesKelahiran(1330-06-15)15 Juni 1330Istana Woodstock, OxfordshireKematian8 Juni 1376(1376-06-08) (umur 45)Istana Westminster, LondonPemakaman29 September 1376Katedral Canterbury, KentWangsaPlantagenetAyahEdward III dari InggrisIbuPhilippa dari HainaultPasanganJoan, Countess of Kent ke-4 (m. invalid year)Anakselengkapnya...Edward dari Angoulêm…

Komedi bersih adalah genre komedi yang umumnya bebas dari kata-kata kasar: rasisme, lelucon seksual, kata-kata yang merendahkan, kata-kata kotor, kecabulan, inses, obat-obatan terlarang, humor yang tidak senonoh, humor toilet, konten seksual yang eksplisit, dan materi yang tidak pantas serupa.[1][2][3][4] Komedian mungkin mencoba menghindari pembatasan komedi bersih dengan menggunakan sindiran, eufemisme, ucapan ganda, maksud ganda, dan bahasa yang netral gender. …

Peta Kabupaten Supiori di Kawasan Indonesia Timur Berikut ini adalah daftar distrik dan kampung di Kabupaten Supiori, Provinsi Papua. Kabupaten Supiori terdiri atas 5 distrik dan 38 kampung dengan luas wilayah 678,32 km² dan jumlah penduduk 21.014 jiwa (2017). Kode Wilayah Kabupaten Supiori adalah 91.19.[1][2][3] Daftar kecamatan dan kelurahan di Kabupaten Supiori adalah sebagai berikut: Kode Wilayah Nama Distrik Ibu kota Jumlah Kampung Daftar 91.19.01 Supiori Selatan Ma…

Penaklukan kembali KonstantinopelBagian dari Peperangan Nikea-LatinGerbang Musim Semi, gerbang yang dilalui tentara Nikea pada saat penaklukan kembali KonstantinopelTanggal25 Juli 1261LokasiKonstantinopelHasil Tentara Nikea memasuki kota tanpa perlawanan Runtuhnya Kekaisaran Latin Restorasi Kekaisaran BizantiumPihak terlibat Kekaisaran Nikea Kekaisaran Latin Republik VenesiaTokoh dan pemimpin Alexios Strategopoulos Baudouin II Penaklukan kembali Konstantinopel adalah perebutan kembali kota Konst…

Artikel ini bukan mengenai orang Moro. Untuk kegunaan lain, lihat Bangsamoro (disambiguasi). Bangsamoro باڠسامورو aDaerah otonomWilayah Otonomi Bangsamoro di Mindanao Muslim Filipino:Rehiyong Awtonomo ng Bangsamoro sa Muslim MindanaoArab:منطقة بانجسامورو ذاتية الحكم فى مسلمى مينداناو BenderaLambangHimne daerah: Himne Bangsamoro Lokasi Bangsamoro di FilipinaOpenStreetMapNegaraFilipinaDidirikan21 Januari 2019Ibu kotaKota Cotabato[1&…

Trem di Hannover, Jerman. Trem atau tram merupakan kereta yang memiliki rel khusus di dalam kota. Trem yang berselang waktu 5-10 menit berangkat, bisa merupakan solusi untuk kemacetan.[1][2] Rangkaian trem umumnya satu set (terdiri atas dua kereta) agar tidak terlalu panjang. Disebut Light Rail karena memakai kereta ringan sekitar 20 ton seperti bus, tidak seberat kereta api yang 40 ton. Letak rel berbaur dengan lalu-lintas kota, atau terpisah seperti bus-way, bahkan bisa pula la…

Cet article est une ébauche concernant un cours d'eau de France et la Seine-et-Marne. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. ru de Vannetinru de Piétrée Le Vannetin à Chartronges. Caractéristiques Longueur 18,6 km [1] Bassin 20 km2 Bassin collecteur Seine Débit moyen 1,1 m3/s (Saint-Siméon) Nombre de Strahler 2 Régime pluvial océanique Cours Source source · Localisation Leudon-en-Br…

UFC mixed martial arts event in 2014 UFC 176: Aldo vs. Mendes IIThe poster for UFC 176: Aldo vs. Mendes IIInformationPromotionUltimate Fighting ChampionshipDateAugust 2, 2014 (cancelled)VenueStaples CenterCityLos Angeles, CaliforniaEvent chronology UFC on Fox: Lawler vs. Brown UFC 176: Aldo vs. Mendes II UFC Fight Night: Bader vs. Saint Preux UFC 176: Aldo vs. Mendes II was a planned mixed martial arts event that was scheduled to be held by the Ultimate Fighting Championship on August 2, 2014, a…

Failed Russian lunar lander Luna-25Luna 25 lunar lander mock-upNamesLuna-Glob landerMission typeTechnology, reconnaissanceOperatorSRI RAS (IKI RAN)COSPAR ID2023-118A SATCAT no.57600Websiteiki.cosmos.ru/missions/luna-25Mission duration1 year (planned)Actual: c. 9 days (mission failure)[1] Spacecraft propertiesSpacecraft typeRobotic landerManufacturerNPO LavochkinLaunch mass1,750 kg (3,860 lb)[2]Payload mass30 kg (66 lb) Start of missionLaunch date23:10:57.1…

1980s in music in the UK Number-one singlesNumber-one albumsBest-selling singlesBest-selling albums Events 1980 1981 1982 1983 1984 1985 1986 1987 1988 1989 ←1970s 1990s→ Australian singer and actor Jason Donovan (pictured in 2007) had six UK top 10 hits in 1989, the most of any artist. These included his number-one solo hits Too Many Broken Hearts and Sealed with a Kiss, as well as his guest appearance with Band Aid II on Do They Know It's Christmas?. Caron Wheeler provided vocals on Soul I…

Serranía de las QuinchasSerranía de las Quinchas Highest pointElevation1,700 m (5,600 ft)Coordinates05°56′00″N 74°11′00″W / 5.93333°N 74.18333°W / 5.93333; -74.18333GeographyCountryColombiaRegionBoyacá, Santander The Serranía de las Quinchas is an 860 km2 area of tropical rainforest and cloud forest in Colombia. It lies in the mid Magdalena River Valley in the foothills of the Cordillera Oriental of the Colombian Andes. It ranges in alt…
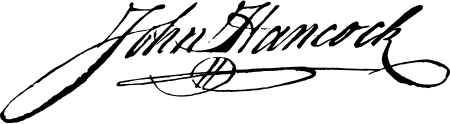
Disambiguazione – Se stai cercando altri significati, vedi Firma (programmazione) o Signature. Firma di Napoleone La firma è la sottoscrizione del proprio nome, o di uno pseudonimo, per chiudere un'opera d'arte o una scrittura, confermarla o renderne noto l'autore.[1] Per questo motivo caratteristiche fondamentali della firma sono la sua unicità e il suo carattere personale. Il termine deriva dalla parola latina firmus, nel senso di definito, inamovibile. Indice 1 Descrizione 1.1…

Commune in Auvergne-Rhône-Alpes, FranceUsson-en-ForezCommune Coat of armsLocation of Usson-en-Forez Usson-en-ForezShow map of FranceUsson-en-ForezShow map of Auvergne-Rhône-AlpesCoordinates: 45°23′27″N 3°56′32″E / 45.3908°N 3.9422°E / 45.3908; 3.9422CountryFranceRegionAuvergne-Rhône-AlpesDepartmentLoireArrondissementMontbrisonCantonSaint-Just-Saint-RambertIntercommunalityLoire Forez AgglomérationGovernment • Mayor (2020–2026) Hervé Beal&…

Artikel ini membutuhkan rujukan tambahan agar kualitasnya dapat dipastikan. Mohon bantu kami mengembangkan artikel ini dengan cara menambahkan rujukan ke sumber tepercaya. Pernyataan tak bersumber bisa saja dipertentangkan dan dihapus.Cari sumber: Rafik Hariri – berita · surat kabar · buku · cendekiawan · JSTOR (February 2011) Rafik Hariri رفيق حريري Perdana Menteri LebanonMasa jabatan31 Oktober 1992 – 2 Desember 1998PendahuluRashid el…

Франц Саксен-Кобург-Заальфельдскийнем. Franz von Sachsen-Coburg-Saalfeld герцог Саксен-Кобург-Заальфельдский 8 сентября 1800 — 9 декабря 1806 Предшественник Эрнст Фридрих Саксен-Кобург-Заальфельдский Преемник Эрнст I Саксен-Кобург-Заальфельдский Рождение 15 июля 1750(1750-07-15)Кобург, Саксе�…
2020年夏季奥林匹克运动会波兰代表團波兰国旗IOC編碼POLNOC波蘭奧林匹克委員會網站olimpijski.pl(英文)(波兰文)2020年夏季奥林匹克运动会(東京)2021年7月23日至8月8日(受2019冠状病毒病疫情影响推迟,但仍保留原定名称)運動員206參賽項目24个大项旗手开幕式:帕维尔·科热尼奥夫斯基(游泳)和马娅·沃什乔夫斯卡(自行车)[1]闭幕式:卡罗利娜·纳亚(皮划艇)[2…

Biblical Psalm This article is about Psalm 83 in Hebrew (Masoretic) numbering. For Psalm 83 in Greek Septuagint or Latin Vulgate numbering, see Psalm 84. Psalm 83Keep not thou silence, O GodPsalm 83 in the King James BibleOther namePsalm 82Deus quis similis erit tibi ne taceasTextby AsaphLanguageHebrew (original) Psalm 83← Psalm 82Psalm 84 →BookBook of PsalmsHebrew Bible partKetuvimOrder in the Hebrew part1CategorySifrei EmetChristian Bible partOld TestamentOrder in the Christian p…

本條目存在以下問題,請協助改善本條目或在討論頁針對議題發表看法。 此條目可参照英語維基百科相應條目来扩充。若您熟悉来源语言和主题,请协助参考外语维基百科扩充条目。请勿直接提交机械翻译,也不要翻译不可靠、低品质内容。依版权协议,译文需在编辑摘要注明来源,或于讨论页顶部标记{{Translated page}}标签。 此條目需要編修,以確保文法、用詞、语气、格式�…

سنة مجريةمعلومات عامةالنوع وحدة زمن تستخدم لقياس المدة الزمنية رمز الوحدة gal (بالإنجليزية) تحويلات الوحدةإلى النظام الدولي 7494930000000000 ثانية الوحدة القياسية 237500000 سنة تعديل - تعديل مصدري - تعديل ويكي بيانات السنة المجرية والتي تعرف أيضًا باسم السنة الكونية، هي مدة الوقت اللازم…
































