Théorème de Routh

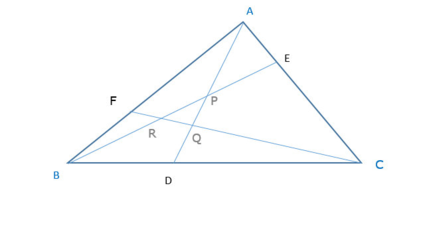
En géométrie euclidienne, le théorème de Routh exprime le rapport entre l'aire d'un triangle et celle du triangle formé par trois céviennes.

Soit un triangle ABC. Trois céviennes issues des trois sommets coupent les côtés opposés en ${\displaystyle D,E,F}$, et découpent un triangle PQR.

Si l'on pose : ${\displaystyle x={\dfrac {\overline {DC}}{\overline {DB}}}}$, ${\displaystyle y={\dfrac {\overline {EA}}{\overline {EC}}}}$, ${\displaystyle z={\dfrac {\overline {FB}}{\overline {FA}}}}$, alors les aires des triangles orientés ${\displaystyle ABC}$ et ${\displaystyle PQR}$ sont reliées par la formule : ${\displaystyle S_{PQR}=S_{ABC}\times {\dfrac {(xyz-1)^{2}}{(xz+x+1)(yx+y+1)(zy+z+1)}}}$^[1]

• Remarque : si les céviennes sont concourantes, l'aire du triangle est nulle, et l'on retrouve le théorème de Ceva (xyz = 1).
• Application : si x = y = z = 2, le rapport est de 1/7, triangle central du partage du triangle en sept triangles de même aire.

Dans le cas où le triangle ${\displaystyle PQR}$ est intérieur au triangle ${\displaystyle ABC}$, on applique le théorème de Ménélaüs au triangle ABD, coupé par la droite (CF) : ${\displaystyle {\dfrac {FA}{FB}}\times {\dfrac {CB}{CD}}\times {\dfrac {QA}{QD}}=1}$. D'où ${\displaystyle {\dfrac {QA}{QD}}={\dfrac {FB}{FA}}\times {\dfrac {CD}{CB}}={\dfrac {zx}{x+1}}}$.

L'aire du triangle AQC vaut ${\displaystyle S_{AQC}={\dfrac {AQ}{AD}}\times S_{ADC}={\dfrac {AQ}{AD}}\times {\dfrac {DC}{BC}}\times S_{ABC}={\dfrac {x}{zx+x+1}}\times S_{ABC}}$

Par permutation circulaire, on obtient ${\displaystyle S_{APB}={\dfrac {y}{xy+y+1}}S_{ABC}}$ et ${\displaystyle S_{BRC}={\dfrac {z}{yz+z+1}}S_{ABC}}$ .

L'aire du triangle PQR vaut donc : ${\displaystyle S_{PQR}=S_{ABC}-S_{AQC}-S_{APB}-S_{BRC}=S_{ABC}\times \left(1-{\dfrac {x}{zx+x+1}}-{\dfrac {y}{xy+y+1}}-{\dfrac {z}{yz++1}}\right)}$

Ou encore ${\displaystyle S_{PQR}=S_{ABC}\times {\dfrac {(xyz-1)^{2}}{(xz+x+1)(yx+y+1)(zy+z+1)}}}$.

Une démonstration utilisant les coordonnées barycentriques et les déterminants permet d'avoir le cas général^[1].

Ce théorème porte le nom du mathématicien anglais Edward Routh, professeur à l'université de Cambridge, plus connu pour ses travaux sur la stabilité des systèmes d'équations différentielles (cf. le critère de Routh-Hurwitz^[2]).

Routh donne ce théorème en 1891 dans A Treatise of Analytical Statics^[3], puis le reprend dans son édition de 1896^[4], édition plus répandue à laquelle les mathématiciens se réfèrent.

Cependant, ce problème apparaît dès 1879 dans Solutions of the Cambridge Senate-House Problems and Riders for the year 1878^[5], recueil d'exercices et de problèmes mathématiques destiné aux étudiants de Cambridge. La correction, donc la preuve du théorème, est due à J. W. L. Glaisher^[6].

Ce problème a donné lieu à de nombreuses démonstrations, dont on trouvera des exemples et une bibliographie dans l'article de Murray S. Klamkin et A. Liu " Three more Proofs of Routh's Theorem" dans Crux Mathematicorum^[7], août 1981, pages 199 et suivantes.

En 2011, Ayoub B. Ayoub publie une nouvelle preuve dans l'article "Routh's theorem revisited", Mathematical Spectrum ^[8].

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Routh's theorem » (voir la liste des auteurs).

• (en) Murray S. Klamkin et A. Liu, « Three more proofs of Routh's theorem », Crux Mathematicorum, vol. 7, n^o 7,‎ 1981, p. 199–203 (lire en ligne).
• H. S. M. Coxeter (1969) Introduction to Geometry, énoncé p. 211, démonstration pp. 219–20, 2nd édition, Wiley, New York.
• (en) J. S. Kline et D. Velleman, « Yet another proof of Routh's theorem », Crux Mathematicorum, vol. 21, n^o 2,‎ 1995, p. 37–40 (lire en ligne)
• Routh's Theorem, Jay Warendorff, The Wolfram Demonstrations Project.
• (en) Eric W. Weisstein, « Routh's Theorem », sur MathWorld
• Routh’s Formula by Cross Products sur MathPages
• Ayoub, Ayoub B. (2011/2012) «Routh's theorem revisited», Mathematical Spectrum 44 (1): 24-27.

• Portail de la géométrie