此條目需要編修，以確保文法、用詞、语气、格式、標點等使用恰当。 (2017年1月21日) 請按照校對指引，幫助编辑這個條目。（幫助、討論）

十二平均律（英語：12 equal temperament），又稱十二等程律，音樂律式的一種，也是當今最主流的律式。將一個八度平均分成十二等份，每等分稱為半音，音高八度音指的是頻率乘上二倍。八度音的頻率分為十二等分，即是分為十二項的等比數列，也就是每個音的頻率為前一個音的2的12次方根倍：

其近似值約為${\displaystyle \,{\sqrt[{12}]{2}}=2^{\frac {1}{12}}\approx \,}$${\displaystyle 1.0594630943593}$ 倍。

公元400年左右，中国南朝数学家何承天提出世界历史上最早有记载的十二平均律数列 900 849 802 758 715 677 638 601 570 536 509.5 479 450（原文：……黄钟长九寸，太簇长八寸二厘，林钟长六寸一厘，应钟长四寸七分九厘强）^[1]。

意大利的物理学家伽利略·伽利莱的父亲溫琴佐·伽利萊（英语：Vincenzo Galilei）曾试图解决十二平均率问题，但他用的倍率是18:17，而不是${\displaystyle {\sqrt[{12}]{2}}}$，因此自乘12次后只得1.98556，不是2，他的系统只可算近似十二音阶平均律^[2]。

1605年荷兰数学家西蒙·斯特芬在一篇未完成的手稿“Van de Spiegheling der singconst”^[3]提出用${\displaystyle {\sqrt[{12}]{1/2}}}$ 计算十二平均律，但因计算精度不够，他算出的弦长数字，有些偏离正确数字一至二单位之多^[4]。

西蒙·斯特芬的弦长表^[5]：

西蒙·斯特芬的频率比，每音一率，且各不相同，这是不正确的^[6]。

中國明代音樂家朱載堉於萬曆十二年（1584年）首次提出「新法密率」（見《律呂精義》、《樂律全書》），推算出以比率 ${\displaystyle {\sqrt[{12}]{2}}}$ 將八度音等分為十二等分的算法，並製造出十二平均律律管及律準，是世界上最早的十二平均律樂器。他用九九八十一位算盘计算出来准确到25位数字新法密率为：

• 
• 
• 
• 
  朱載堉新法密率
• 
• 
• 

朱載堉为了验证所创的十二平均律理论，计算出所需的长度和律管内径，特选用上等竹子，按数据截取所需的长度，按数据镟出内径，分别创制世界上最早的十二平均律律管36根，分别为新法密率倍率管12根、正律管12根和半律管12根^[7]。选上好竹子制造，金门竹、班竹或紫竹都可，而當時朱載堉採用的是江南出产的笔管竹。

倍率黄钟管的内径取为五寸，下一根竹管的内径为上根竹管的直径除以${\displaystyle {\sqrt[{24}]{2}}}$：

倍率黄钟管的内径取为五寸，下一根竹管的内径为上根竹管的直径除以${\displaystyle {\sqrt[{24}]{2}}}$。

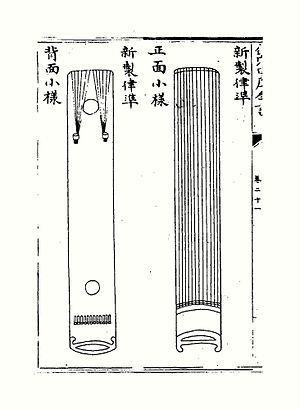
朱載堉依他對十二平均律所發明的新法密率理論，创制一種律准。用桐木制作，琴身厚四分，张琴弦12根，琴底藏一根黄钟律管，用来定黄钟^[8]。

按第 1 弦为 黃鐘 与本弦 散声 应

按第 2 弦为 大呂 与本弦 散声 应

按第 3 弦为 太蔟 与本弦 散声 应

按第 4 弦为 夾鍾 与本弦 散声 应

按第 5 弦为 姑洗 与本弦 散声 应

按第 6 弦为 仲呂 与本弦 散声 应

按第 7 弦为 蕤賓 与本弦 散声 应

按第 8 弦为 林鍾 与本弦 散声 应

按第 9 弦为 夷則 与本弦 散声 应

按第 10 弦为 南呂 与本弦 散声 应

按第 11 弦为 無射 与本弦 散声 应

按第 12 弦为 應鍾 与本弦 散声 应

16世纪末叶中外交通方兴未艾，1580年开始，明朝广东承宣布政使司每两年在广州举办一次为时数周的交易会，届时东西商人和传教士會交流货物和思想；^[9]朱載堉刊行十二平均律学说之时，正值耶稣会意大利传教士利马窦来华之时，利马窦在其私人日记里提到朱載堉的历法新理论，利马窦本人又是精通天文学和数学，很可能知道朱載堉用${\displaystyle {\sqrt[{12}]{2}}}$来解决春分与夏至三个月之间的比率：无独有偶，利马窦还是法国位居高位的科学家马兰·梅森 （Pere Marin Mersenne）的朋友，他们有共同的学术兴趣，因此卓仁祥認為，在他们交往过程中，利马窦将朱載堉获得的${\displaystyle {\sqrt[{12}]{2}}}$=1.059463094359295264561825 传达给梅森。1638年梅森出版《和谐音概论（英语：Harmonie universelle）》，书中在西方世界第一次出现1.059463 这个数字，在此之前西方无人知道这个数字^[2]。

十九世纪德国物理学家赫尔曼·冯·亥姆霍兹在所著的论音感一书中写道：“中国有一位王子名叫載堉，力排众议，创导七声音阶。而将八度分成十二个半音的方法，也是这个富有天才和智巧的国家发明的”^[10]。1890年布鲁塞尔皇家音乐博物馆馆长 Victor Charles Mahillon 按朱載堉十二平均律律管数据，复制了一套律管，经过测试之后，他写道：“关于乐管的管径，我们毫无所知，中国人比我们知道的多得多。我们按王子載堉的数据复制了一套律管，测试结果表明他的理论的准确性”^[11]。

德国作曲家巴赫於1722年發表的《平均律键盘曲集》(Das Wohltemperierten Klavier，中文意思是「完美調音的鍵盤樂器」)，雖然現代中文翻譯為「平均律」，但可能並不是為使用十二平均律的鍵盤樂器而著。十二平均律的德文是Gleichschwebende Temperatur，而不是Wohltemprierte。平均律的英文是Equal Temperament，Temperament是Temper（調律）的動詞，因為百餘年來歐美各國的調律都採十二平均律，故現在習慣以Temperament表示十二平均律。

James Murray Barbour (1897, 3, 31 - 1970, 1, 04) 研究「調律技術演進史」，認為1842年由英國樂器製造廠Broadwood找到十二平均律的調律法，十二平均律才能普及。^[12] 巴赫的鍵盤樂器则是使用他的学生，音乐理论家Johann Philipp Kirnberger（英语：Johann Kirnberger）綜合中庸全音律與五度相生律的原理，所發明的調律法。

朱載堉显然是历史上最先获得准确的100音分半音十二平均律的人；半世纪之后德国数学家Johann Faulhaber也获得了准确的100音分。

將主音設為a1(440Hz)，來計算所有音的頻率，結果如下 （为计算过程更清晰，分数不进行约分）：

音程名稱	間隔半音數	十二平均律的倍數	頻率
纯一度(A1)	0	${\displaystyle 2^{0}=1\,}$	${\displaystyle 440\times 1=440\,}$
增一度/小二度(A♯1/B♭1)	1	${\displaystyle {\sqrt[{12}]{2}}=2^{\frac {1}{12}}\approx 1.0594630943592952645618252949463}$	${\displaystyle 440\times 2^{\frac {1}{12}}\approx 466.1637615180899164072031297762}$
大二度(B1)	2	${\displaystyle {\sqrt[{6}]{2}}=2^{\frac {2}{12}}\approx 1.1224620483093729814335330496792}$	${\displaystyle 440\times 2^{\frac {2}{12}}\approx 493.8833012561241118307545418586}$
小三度(C)	3	${\displaystyle {\sqrt[{4}]{2}}=2^{\frac {3}{12}}\approx 1.1892071150027210667174999705605}$	${\displaystyle 440\times 2^{\frac {3}{12}}\approx 523.2511306011972693556999870466}$
大三度(C♯)	4	${\displaystyle {\sqrt[{3}]{2}}=2^{\frac {4}{12}}\approx 1.2599210498948731647672106072782}$	${\displaystyle 440\times 2^{\frac {4}{12}}\approx 554.3652619537441924975726672023}$
纯四度(D)	5	${\displaystyle {\sqrt[{12}]{32}}=2^{\frac {5}{12}}\approx 1.3348398541700343648308318811845}$	${\displaystyle 440\times 2^{\frac {5}{12}}\approx 587.3295358348151205255660277209}$
增四度/減五度(D#/E♭)	6	${\displaystyle {\sqrt {2}}=2^{\frac {6}{12}}\approx 1.4142135623730950488016887242097}$	${\displaystyle 440\times 2^{\frac {6}{12}}\approx 622.2539674441618214727430386522}$
纯五度(E)	7	${\displaystyle {\sqrt[{12}]{128}}=2^{\frac {7}{12}}\approx 1.4983070768766814987992807320298}$	${\displaystyle 440\times 2^{\frac {7}{12}}\approx 659.2551138257398594716835220930}$
小六度(F)	8	${\displaystyle {\sqrt[{3}]{4}}=2^{\frac {8}{12}}\approx 1.5874010519681994747517056392723}$	${\displaystyle 440\times 2^{\frac {8}{12}}\approx 698.4564628660077688907504812795}$
大六度(F#)	9	${\displaystyle {\sqrt[{4}]{8}}=2^{\frac {9}{12}}\approx 1.6817928305074290860622509524664}$	${\displaystyle 440\times 2^{\frac {9}{12}}\approx 739.9888454232687978673904190852}$
小七度(G)	10	${\displaystyle {\sqrt[{6}]{32}}=2^{\frac {10}{12}}\approx 1.781797436280678609480452411181}$	${\displaystyle 440\times 2^{\frac {10}{12}}\approx 783.9908719634985881713990609195}$
大七度(G#)	11	${\displaystyle {\sqrt[{12}]{2048}}=2^{\frac {11}{12}}\approx 1.8877486253633869932838263133351}$	${\displaystyle 440\times 2^{\frac {11}{12}}\approx 830.6093951598902770448835778670}$
纯八度(A)	12	${\displaystyle 2^{1}=2\,}$	${\displaystyle 440\times 2=880\,}$

其中${\displaystyle \,{\sqrt[{12}]{2}}=2^{\frac {1}{12}}\approx \,}$${\displaystyle 1.0594630943593}$

${\displaystyle \approx {\frac {18}{17}}=1.05882}$ 99 音分

${\displaystyle \approx {\frac {107}{101}}=1.05941}$ 99.9 音分

${\displaystyle \approx {\frac {11011}{10393}}=1.05946310}$ 100 音分

• 李約瑟：《中國科學技術史》第四卷第一分册
• Robert Temple：The Genius of CHINA （李約瑟《中國科學技術史》的濃縮本）
• 戴念祖：《朱载堉———明代的科学和艺术巨星》
• 程貞一 著，王翼勳 譯：《黃鐘大呂：中國古代和十六世紀聲學成就》（上海：上海科技教育出版社，2007）。
• Cho, Gene Jinsiong. (2003). The Discovery of Musical Equal Temperament in China and Europe in the Sixteenth Century. Lewiston, NY: The Edwin Mellen Press.

• 十二律
• 律学
• 朱載堉