在残差神经网络中的一个残差块里,残差连接跳过了两个网络层。 残差神经网络 (Residual Neural Network ,简称ResNet )[ 1] 高速神经网络 [ 2] 长短期记忆 模型LSTM、[ 3] Transformer模型 (比如BERT 和GPT 系列,ChatGPT 等)、AlphaGo Zero 、AlphaStar AlphaFold 等。
残差神经网络由何恺明 、张祥雨、任少卿和孙剑开发,这一成果在2015年的ImageNet 大规模视觉识别挑战赛中夺冠。[ 4] [ 5]
2012年,针对ImageNet 竞赛开发的AlexNet 模型是一个包含8层的卷积神经网络 。到了2014年,牛津大学 的视觉几何组(VGG)通过叠加3x3卷积层将网络深度增加到了19层。[ 6] [ 7] [ 1]
理论上,如果一个更深的网络仅仅是通过在一个较浅网络的基础上增加额外层来构建的,那么这个更深的网络不应该比其较浅的网络有更高的训练损失。[ 1]
在多层神经网络模型里,设想一个包含若干层的子网络。这个子网络的函数用
H
(
x
)
{\textstyle H(x)}
x
{\textstyle x}
F
(
x
)
:=
H
(
x
)
−
x
{\textstyle F(x):=H(x)-x}
y
{\textstyle y}
y
=
F
(
x
)
+
x
{\displaystyle {\begin{aligned}y&=F(x)+x\end{aligned}}}
这一原理同样适用于1997年提出的长短期记忆 LSTM单元,[ 3] 随时间反向传播
y
t
+
1
=
F
(
x
t
)
+
x
t
{\textstyle y_{t+1}=F(x_{t})+x_{t}}
y
=
F
(
x
)
+
x
{\textstyle y=F(x)+x}
函数
F
(
x
)
{\textstyle F(x)}
激活函数 以及规范化操作(如批量规范化
这类子网络被称作“残差块”。[ 1]
在"
y
=
F
(
x
)
+
x
{\textstyle y=F(x)+x}
+
x
{\textstyle +\ x}
[ 8]
身份映射的引入有利于信号在前向传播路径和反向传播路径中的传递。[ 9]
如果第
ℓ
{\textstyle \ell }
(
ℓ
+
1
)
{\textstyle (\ell +1)}
[ 9]
x
ℓ
+
1
=
F
(
x
ℓ
)
+
x
ℓ
{\displaystyle {\begin{aligned}x_{\ell +1}&=F(x_{\ell })+x_{\ell }\end{aligned}}}
若递归应用此公式,例如,
x
ℓ
+
2
=
F
(
x
ℓ
+
1
)
+
x
ℓ
+
1
=
F
(
x
ℓ
+
1
)
+
F
(
x
ℓ
)
+
x
ℓ
{\displaystyle {\begin{aligned}x_{\ell +2}=F(x_{\ell +1})+x_{\ell +1}=F(x_{\ell +1})+F(x_{\ell })+x_{\ell }\end{aligned}}}
x
L
=
x
ℓ
+
∑
i
=
l
L
−
1
F
(
x
i
)
{\displaystyle {\begin{aligned}x_{L}&=x_{\ell }+\sum _{i=l}^{L-1}F(x_{i})\\\end{aligned}}}
这里
L
{\textstyle L}
ℓ
{\textstyle \ell }
ℓ
{\textstyle \ell }
L
{\textstyle L}
残差学习的公式还在一定程度上缓解了梯度消失问题 。然而,梯度消失并不是导致性能退化问题的根源,因为通过引入规范化层(如批量规范化)可在一定程度上解决此问题。根据上面的前向传播过程,对
x
ℓ
{\textstyle x_{\ell }}
[ 9]
∂
E
∂
x
ℓ
=
∂
E
∂
x
L
∂
x
L
∂
x
ℓ
=
∂
E
∂
x
L
(
1
+
∂
∂
x
ℓ
∑
i
=
l
L
−
1
F
(
x
i
)
)
=
∂
E
∂
x
L
+
∂
E
∂
x
L
∂
∂
x
ℓ
∑
i
=
l
L
−
1
F
(
x
i
)
{\displaystyle {\begin{aligned}{\frac {\partial {\mathcal {E}}}{\partial x_{\ell }}}&={\frac {\partial {\mathcal {E}}}{\partial x_{L}}}{\frac {\partial x_{L}}{\partial x_{\ell }}}\\&={\frac {\partial {\mathcal {E}}}{\partial x_{L}}}\left(1+{\frac {\partial }{\partial x_{\ell }}}\sum _{i=l}^{L-1}F(x_{i})\right)\\&={\frac {\partial {\mathcal {E}}}{\partial x_{L}}}+{\frac {\partial {\mathcal {E}}}{\partial x_{L}}}{\frac {\partial }{\partial x_{\ell }}}\sum _{i=l}^{L-1}F(x_{i})\\\end{aligned}}}
这里
E
{\textstyle {\mathcal {E}}}
∂
E
∂
x
ℓ
{\textstyle {\frac {\partial {\mathcal {E}}}{\partial x_{\ell }}}}
∂
E
∂
x
L
{\textstyle {\frac {\partial {\mathcal {E}}}{\partial x_{L}}}}
∂
E
∂
x
L
{\textstyle {\frac {\partial {\mathcal {E}}}{\partial x_{L}}}}
F
(
x
i
)
{\textstyle F(x_{i})}
∂
E
∂
x
ℓ
{\textstyle {\frac {\partial {\mathcal {E}}}{\partial x_{\ell }}}}
两种类型的卷积残差块。左侧是基本块,它由两个3x3卷积层组成。右侧是瓶颈块,该块先通过一个1x1卷积层进行降维,接着是一个3x3卷积层,最后再通过一个1x1卷积层恢复原来的维度。
基本残差块是原始ResNet研究中最简单的部分。[ 1] 卷积层 以及一个残差连接。这两层的输入输出尺寸保持一致。
瓶颈残差块包含三个串联的卷积层和一个残差连接。[ 1] [ 1]
预激活残差块[ 9]
F
{\textstyle F}
x
ℓ
+
1
=
F
(
ϕ
(
x
ℓ
)
)
+
x
ℓ
{\displaystyle {\begin{aligned}x_{\ell +1}&=F(\phi (x_{\ell }))+x_{\ell }\end{aligned}}}
这里的
ϕ
{\textstyle \phi }
线性整流函数 等任意非线性激活或归一化操作。这种设计减少了残差块间非恒等映射的数量,被用于训练200层到1000多层的模型。[ 9]
从GPT-2 开始,Transformer 块常被用于预激活块,这在Transformer模型的相关文献中被称为“预规范化”。[ 10]
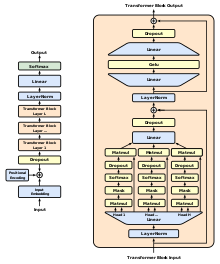
原始GPT 模型采用的Transformer 架构是由两种类型的残差块构成:一个是多头注意力块,另一个是前馈的多层感知器 (MLP)块。这种设计通过结合两个功能强大的残差块,使得Transformer能够高效地处理数据并学习复杂的特征,其中每个残差块都利用残差连接来促使信号在网络深层之间的流动以及更有效的进行梯度回传,克服了深度模型训练过程中遇到的梯度消失等问题。 Transformer块是由两个残差块组成,每个残差块都设有一个残差连接。
第一个残差块为多头注意力块,使用了自注意力运算,随后连接一个线性映射层。第二个残差块是一个前馈式的多层感知器 (MLP)块,这个块在某种程度上像是一个“反向”的瓶颈块,它通过一个线性映射层(在卷积神经网络中相当于1x1的卷积)来扩大维度,然后通过另一个线性映射层来减少维度。
一个Transformer块包含了四层线性映射。GPT-3 模型拥有96个这样的Transformer块(在Transformer领域的文献中,通常将一个Transformer块称作一个“Transformer层”)。因此,该模型包含了大约400层的映射层,包括Transformer块内的96x4层,以及一些额外的层用于输入嵌入和输出预测。
若没有残差连接,训练网络深度极高的Transformer模型将无法取得成功。[ 11]
1961年,在弗兰克·罗森布拉特 出版的书籍中介绍了一个含有跳跃连接的三层多层感知器 (MLP)模型(详见第15章,第313页[ 12] [ 12]
在1994年[ 13] [ 14] [ 13] [ 14] [ 13]
塞普·霍赫赖特 梯度消失问题 ,并认为这是深度学习 效果不佳的原因。[ 15] 长短期记忆 (LSTM)网络[ 3]
y
t
+
1
=
F
(
x
t
)
+
x
t
{\textstyle y_{t+1}=F(x_{t})+x_{t}}
随时间反向传播
y
=
F
(
x
)
+
x
{\textstyle y=F(x)+x}
循环神经网络 的有效训练。2000年[ 16] [ 16]
2015年,高速神经网络 [ 2] [ 17] 前馈神经网络 ,被媒体报道称为“首个具有数百层深度的前馈神经网络 ”。[ 18] [ 2] [ 2] [ 2] [ 9] [ 9] [ 16] Transformer )中使用的跳跃连接主要就是身份映射。
2016年出现的DenseNets[ 19]
利用残差网络架构,实现了具有随机深度的神经网络。[ 20] 视觉Transformer
虽然最初的残差网络研究并未受生物学 启发,但后来的研究却发现残差网络与生物学有关。[ 21] [ 22]
2023年《科学 》杂志上发表的一项研究展示了果蝇 幼虫 大脑 的完整神经连接组 。[ 23]
^ 1.0 1.1 1.2 1.3 1.4 1.5 1.6 He, Kaiming; Zhang, Xiangyu; Ren, Shaoqing; Sun, Jian. Deep Residual Learning for Image Recognition. 10 Dec 2015. arXiv:1512.03385 ^ 2.0 2.1 2.2 2.3 2.4 Srivastava, Rupesh Kumar; Greff, Klaus; Schmidhuber, Jürgen. Highway Networks. 3 May 2015. arXiv:1505.00387 cs.LG ]. ^ 3.0 3.1 3.2 Sepp Hochreiter; Jürgen Schmidhuber . Long short-term memory . Neural Computation. 1997, 9 (8): 1735–1780 [2024-01-27 ] . PMID 9377276 S2CID 1915014 doi:10.1162/neco.1997.9.8.1735 存档 于2021-01-22). ^ Deng, Jia; Dong, Wei; Socher, Richard; Li, Li-Jia; Li, Kai; Fei-Fei, Li. ImageNet: A large-scale hierarchical image database . CVPR. 2009 [2024-01-27 ] . (原始内容存档 于2019-09-29). ^ ILSVRC2015 Results . image-net.org. [2024-01-27 ] . (原始内容存档 于2023-09-29). ^ Simonyan, Karen; Zisserman, Andrew. Very Deep Convolutional Networks for Large-Scale Image Recognition. 2014. arXiv:1409.1556 cs.CV ]. ^ He, Kaiming; Zhang, Xiangyu; Ren, Shaoqing; Sun, Jian. Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification. 2016. arXiv:1502.01852 cs.CV ]. ^ Szegedy, Christian; Ioffe, Sergey; Vanhoucke, Vincent; Alemi, Alex. Inception-v4, Inception-ResNet and the impact of residual connections on learning. 2016. arXiv:1602.07261 cs.CV ]. ^ 9.0 9.1 9.2 9.3 9.4 9.5 9.6 He, Kaiming; Zhang, Xiangyu; Ren, Shaoqing; Sun, Jian. Identity Mappings in Deep Residual Networks. 2015. arXiv:1603.05027 cs.CV ]. ^ Radford, Alec; Wu, Jeffrey; Child, Rewon; Luan, David; Amodei, Dario; Sutskever, Ilya. Language models are unsupervised multitask learners (PDF) . 14 February 2019 [19 December 2020] . (原始内容存档 (PDF) 于6 February 2021). ^ Dong, Yihe; Cordonnier, Jean-Baptiste; Loukas, Andreas. Attention is not all you need: pure attention loses rank doubly exponentially with depth. 2021. arXiv:2103.03404 cs.LG ]. ^ 12.0 12.1 Rosenblatt, Frank. Principles of neurodynamics. perceptrons and the theory of brain mechanisms (PDF) . 1961 [2024-01-27 ] . (原始内容存档 (PDF) 于2023-05-04). ^ 13.0 13.1 13.2 Venables, W. N.; Ripley, Brain D. Modern Applied Statistics with S-Plus . Springer. 1994 [2024-01-27 ] . ISBN 9783540943501存档 于2023-08-22). ^ 14.0 14.1 Ripley, B. D. Pattern Recognition and Neural Networks . Cambridge University Press. 1996 [2024-01-27 ] . (原始内容存档 于2023-12-02). ^ Hochreiter, Sepp. Untersuchungen zu dynamischen neuronalen Netzen (PDF) (diploma论文). Technical University Munich, Institute of Computer Science, advisor: J. Schmidhuber. 1991 [2024-01-27 ] . (原始内容存档 (PDF) 于2023-03-20). ^ 16.0 16.1 16.2 Felix A. Gers; Jürgen Schmidhuber; Fred Cummins. Learning to Forget: Continual Prediction with LSTM. Neural Computation. 2000, 12 (10): 2451–2471. CiteSeerX 10.1.1.55.5709 PMID 11032042 S2CID 11598600 doi:10.1162/089976600300015015 ^ Srivastava, Rupesh Kumar; Greff, Klaus; Schmidhuber, Jürgen. Training Very Deep Networks. 22 July 2015. arXiv:1507.06228 cs.LG ]. ^ Schmidhuber, Jürgen. Microsoft Wins ImageNet 2015 through Highway Net (or Feedforward LSTM) without Gates . 2015 [2024-01-27 ] . (原始内容存档 于2023-11-27). ^ Huang, Gao; Liu, Zhuang; van der Maaten, Laurens; Weinberger, Kilian. Densely Connected Convolutional Networks. 2016. arXiv:1608.06993 ^ Huang, Gao; Sun, Yu; Liu, Zhuang; Weinberger, Kilian. Deep Networks with Stochastic Depth. 2016. arXiv:1603.09382 ^
Liao, Qianli; Poggio, Tomaso. Bridging the Gaps Between Residual Learning, Recurrent Neural Networks and Visual Cortex. 2016. arXiv:1604.03640
^
Xiao, Will; Chen, Honglin; Liao, Qianli; Poggio, Tomaso. Biologically-Plausible Learning Algorithms Can Scale to Large Datasets. 2018. arXiv:1811.03567
^ Winding, Michael; Pedigo, Benjamin; Barnes, Christopher; Patsolic, Heather; Park, Youngser; Kazimiers, Tom; Fushiki, Akira; Andrade, Ingrid; Khandelwal, Avinash; Valdes-Aleman, Javier; Li, Feng; Randel, Nadine; Barsotti, Elizabeth; Correia, Ana; Fetter, Fetter; Hartenstein, Volker; Priebe, Carey; Vogelstein, Joshua; Cardona, Albert; Zlatic, Marta. The connectome of an insect brain . Science. 10 Mar 2023, 379 (6636): eadd9330. PMC 7614541 PMID 36893230 S2CID 254070919 bioRxiv 10.1101/2022.11.28.516756v1 doi:10.1126/science.add9330
可微分计算
概论 概念 应用 硬件 软件库 实现
人物 组织 架构