この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。 出典を追加して記事の信頼性向上にご協力ください。（このテンプレートの使い方） 出典検索?: "写像" – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ · TWL (2021年4月)

この項目は内容が専門的であり、一般の閲覧者にはわかりにくくなっているおそれがあります。 専門用語をわかりやすい表現にするための修正をして下さる協力者を求めています。（2021年4月）

写像（しゃぞう、英: mapping, map）は、二つの集合が与えられたときに、一方の集合の各元に対し、他方の集合のただひとつの元を指定して結びつける対応のことである。関数、変換、作用素、射などが写像の同義語として用いられる^[1][2]こともある。

ブルバキに見られるように、写像は集合とともに現代数学の基礎となる道具の一つである。現代的な立場では、「写像」と（一価の）「関数」は論理的におなじ概念を表すものと理解されているが、歴史的には「関数」の語は解析学に出自を持つものであり、一部には必ずしも写像でないものも関数の名の下におなじ範疇に扱われる（多価関数参照）。文献によっては「数の集合（大抵の場合実数体 R または複素数体 C の部分集合）を終域に持つ写像」をして特に「関数」と呼び、「写像」はより一般の場合に用いる^[3][4]。関数、二項関係、対応の各項も参照のこと。

集合 A の各元に対してそれぞれ集合 B の元をただひとつずつ指定するような規則 f が与えられているとき、f を「定義域（あるいは始域） A から終域 B への写像」といい

${\displaystyle f\colon A\to B,\quad A{\stackrel {f}{{}\to {}}}B}$

などと表す。また f は A で（あるいは A の上で）定義されているといい、あるいはまた f は B に（あるいは B の中に）値を持つという。始域 A を sour(f)、終域 B を tar(f) のように記すこともある。また、A の元 a に対して f によって指定される B の元が b である（このことを、a が f によって b に写されるという）とき、b を a における f の像あるいは値（あたい、value）と呼び、b を f(a) で表す。 f によって A の元 a が B の元 f(a) に写されることは、

という記法で表される^[5]。変数 x を用いて x ↦ f(x) のように写像を表すとき、f は、 A をわたる（または動く）変数 x の関数である、あるいは変数 x に従属するという^[要出典]。

2つの写像 f : A→B、 g : A→B の相等関係について、次が成り立つ：

集合論においては、集合 A, B の元の順序対からなる集合（すなわち二項関係）f が

• x ∈ A ならば (x, y) ∈ f を満たす y ∈ B が存在する
• (x, y₁) ∈ f かつ (x, y₂) ∈ f ならば y₁ = y₂

の二つをみたすとき、f を A から B への関数と呼び^[7]、f: A → B で表す。またこのとき、(x, y) ∈ f であることを f(x) = y と書く。この文脈では、f と f のグラフ {(x, y) | y = f(x)} を同一視し、関数と写像を同じ意味に用いる。 二つの写像 f と g の相等は、集合として同一であるということ、すなわち

∀x∀y ( (x,y) ∈ f ⇔ (x,y) ∈ g )

ということであるが、これは（ f と g の定義域が等しく、かつ）任意の a ∈ A に対して f(a) = g(a) であることと同値である。

一方、圏論の用語との整合性を重んじる文脈では、次のようになる。 集合 A, B の元の順序対からなる集合（すなわち二項関係）G_f が

• 全域性: x ∈ A ならば (x, y) ∈ G_f を満たす y ∈ B が存在する
• 右一意または関数的: (x, y₁) ∈ G_f かつ (x, y₂) ∈ G_f ならば y₁ = y₂

の二つをみたすとき、三つ組 f := (A, B, G_f) をこの関数関係 G_f から定まる A から B への写像と呼び、f: A → B で表す。またこのとき、(x, y) ∈ G_f であることを f(x) = y と書き、G_f = {(x, y) | y = f(x)} を写像 f のグラフと呼ぶ。二つの写像 (A, B, G_f) と (C, D, G_g) の相等は、三つ組としての相等をいう。特に、f, g がともに A から B への写像のとき、f と g が等しいというのは、この二つの写像のグラフG_f と G_g とが A × B の集合として同一であるということ、すなわち

∀x∀y ( (x,y) ∈ G_f ⇔ (x,y) ∈ G_g)

ということであるが、これは任意の a ∈ A に対して f(a) = g(a) であることと同値なので、素朴な意味で写像 f と g が等しいと言ったときと同じ意味となる。

圏論の用語と整合性をとる文脈では、写像の相等を扱う際の、二つの写像が「ともに A から B への」写像であるという但し書きは重要である。例えば A から B への写像 f と A から B ⊆ B′ なる B′ への写像 g について、集合として f = g（つまりグラフが一致）でも三つ組としては異なるから、この二つの写像は同一でない。実際、x ↦ x² なる元の対応で定められる二つの写像 f: R → R と g: R → R_≥0 を考えると後者は全射性を持つが前者はそうでない^[8]（値域・終域の各項も参照）。

また、超限帰納法を用いるなどして写像を集合論的に構成する場合、始域や終域としては「すべての集合」のような真の類を考えることもある^[要出典]。そのような場合でも定義域 A を集合に制限すれば順序対の集まり f|_A や値域 f(A) も集合となる^[要出典]。

• 集合 A の任意の元 a に対して a 自身を対応させると、これは A から A への写像になる。この写像を恒等写像といい、I_A や id_A や 1_A などで表す。
• B を A の部分集合とするとき、B の任意の元 b に対して b 自身を A の元として対応させる B から A への写像を包含写像といい、i_{A, B} や inc_{A, B} などで表す。
• f: A → B とする。A の部分集合 A′ について、A′ の各元 a に対して B の元 f(a) を対応させると、これは A′ から B への写像になる。この写像を f の A′ への制限写像といい、f|_A′ と表す。
• A が空集合のとき、A から B への写像はただ一つ存在し、これを空写像と呼ぶ。空写像に対応するグラフは空集合である。A の元が存在しないので何の対応も定めてはいないが、これも立派な写像である。素朴な定義では、f が写像であるとは「a が A の元ならば B の元 f(a) がただ一つ定まる」が成り立つことであったが、A が空集合ならば「a が A の元」は偽であるから、この命題は真である。この議論は A と B が共に空集合である場合も通用するので、空集合から空集合への写像は空写像ただ一つである^{[注釈 1]}。

• x ∈ R に 絶対値 |x| を対応させる |・|: R → [0, ∞) は写像である。これは全射であるが単射ではない。
• GL(n, R) を n 次実一般線型群、即ち正則な実 n 次正方行列の全体とする。行列 A ∈ GL(n, R) にその行列式 ${\displaystyle \det A\in \mathbb {R} ^{\times }:=\mathbb {R} \setminus \{0\}}$ を対応させる対応 det: GL(n, R) → R^× は写像になる。これも全射であるが n ≥ 2 のとき単射ではない。
• R₂[x] を {ax² + bx + c  |  a, b, c ∈ R, a ≠ 0} （実係数2次多項式全体）で定める。多項式 ax² + bx + c ∈ R₂[x] にその判別式 D = b² − 4ac ∈ R を対応させる対応 D: R₂[x] → R は写像である。これも全射であるが単射ではない。
• ${\displaystyle x\in \mathbb {R} }$ に ${\displaystyle \lfloor x\rfloor :=\max\{n\in \mathbb {Z} \mid x\geq n\}}$ （${\displaystyle x}$ 以下の最大の整数）を対応させる対応 ${\displaystyle \lfloor \cdot \rfloor \colon \mathbb {R} \to \mathbb {Z} }$ は床関数といわれる。同様に、${\displaystyle \lceil x\rceil :=\min\{n\in \mathbb {Z} \mid x\leq n\}}$ （${\displaystyle x}$ 以上の最小の整数）を対応させる対応 ${\displaystyle \lceil \cdot \rceil \colon \mathbb {R} \to \mathbb {Z} }$ は天井関数といわれる。どちらも、全射であるが単射ではない。
• ${\displaystyle z=a+bi\in \mathbb {C} }$ に実部, 虚部を対応させる写像 ${\displaystyle \mathrm {Re} \colon \mathbb {C} \ni z\mapsto a\in \mathbb {R} }$, ${\displaystyle \mathrm {Im} \colon \mathbb {C} \ni z\mapsto b\in \mathbb {R} }$ はともに全射であるが単射でない.
• n 個の空でない集合 X₁,...,X_n の直積集合 ${\displaystyle X_{1}\times \cdots \times X_{n}}$ から X_i への写像 p_i を次のように定める: ${\displaystyle p_{i}\colon X_{1}\times \cdots \times X_{n}\ni (x_{1},\dots ,x_{n})\mapsto x_{i}\in X_{i}.}$ これは ${\displaystyle X_{1}\times \cdots \times X_{n}}$ から X_i への第 ${\displaystyle i}$ 射影（${\displaystyle i}$ -th projection）といわれる. これは全射であるが単射でない.

• 線型空間の間の線型写像
• 群や環等の間の準同型写像
• 距離空間や位相空間の間の連続写像
• 順序集合の間の単調写像
• 可微分多様体間の可微分写像

など。これらはどれも、圏論における射の例になっている。（#射・関手）

X, Y を集合とする。写像 f: X → Y が X の任意の元 x, y に対して f(x) = f(y) をみたすとき、f は定値写像といわれる。X が空でないとき、定値写像とはその像が一元集合となるものである。X が空であるときは、文献によって扱いが異なる。

B′ を B の部分集合とするとき、f によって B′ に写される始域 A の元全体からなる集合 {a ∈ A  |  f(a) ∈ B′} を B′ の逆像または原像といい、f⁻¹(B′) で表す^{[注釈 2]}。

A の部分集合 X の元の f による像たちの全体からなる終域 B の部分集合 {f(a)  |  a ∈ X} を X の f による像といい、f[X], f″X などで表す。特に f の A による像 f[A] を f の値域 (range) と呼び、ran(f), Im(f) などで表す^{[注釈 3]}。つまり、写像 f: A → B あるいは G_f ⊆ A × B の値域 ran(f) は

${\displaystyle \operatorname {ran} (f)=\{y\mid \exists x((x,y)\in G_{f})\}\subseteq B}$

で定義される。

2つの写像 f : A→B、 g : B→C が与えられたとする。そのとき、 A の元 a に C の元 g(f(a)) を対応させる A から C への写像が1つ得られる^[9]。その写像を f と g との合成写像（あるいは積）といい、 g∘f（または gf ）で表す：

写像 f : A→B、 g : B→C、 h : C→D が与えられたとき、

• (h∘g)∘f = h∘(g∘f)　　（結合律）、
• f∘I_A = f、　I_B∘f = f

が成り立つ^[10]。（なお、写像の合成について交換律は成り立たない^[11]）これらのことから、特に A からそれ自身への写像（A 上の変換）全体の集合は恒等写像を単位元とする非可換モノイドをなすことがわかる。

右全域性「f: A → B について ran(f) = B」が成り立つとき（つまり値域と終域が一致するとき）、f を A から B への全射という。

左一意性「A の任意の元 a₁, a₂ に対して、a₁ ≠ a₂ ならば f(a₁) ≠ f(a₂)」が成り立つとき、 f を単射という。包含写像は単射である。単射の制限写像も単射である。

A から B への全射 f がさらに単射でもあるとき、f は A から B への全単射であると言われる。定義域を A とする任意の単射 f はあきらかにその値域 f(A) への全単射である。

f を A から B への全単射とする。そのとき、 B の元 b に対して、 f(a) = b であるような A の元 a がちょうど1つ存在する。そこで、 B の元 b にそのような A の元 a を対応させる B から A への写像を f の逆写像といい、f⁻¹ と表す。定義より次が成り立つ：

f⁻¹は B から A への全単射である。f⁻¹ の構成から、

${\displaystyle f^{-1}\circ f=\operatorname {id} _{A},\quad f\circ f^{-1}=\operatorname {id} _{B}}$

であることが分かる。

A からそれ自身への全単射全体の集合を S(A) とすると、写像の合成は結合法則を満たし、恒等写像を単位元として、任意の全単射が逆写像を逆元に持つから、これは群をなす。特に A が n 個の元からなる有限集合の場合の S(A) を n 次対称群という。

f: A → B, g: C → D の合成 g ∘ f: A → D が定義可能で全単射であるとき、g が全射であることおよび f が単射であることが容易に確かめられるが、このことの逆も次の意味で成り立つ。

• f: A → B が全射であるとき、（選択公理を仮定すると）B から A への写像 r が存在して右可逆性 f ∘ r = id_B が成り立つ。この r のことを、f の右逆写像という。
• f: A → B （A ≠ ∅）が単射であるとき、B から A への写像 l が存在して左可逆性 l ∘ f = id_A が成り立つ。この l のことを、f の左逆写像という。

この二つの事実には、正確に逆が成り立つ。従って、全射と単射を次のように定義することもできる；

写像 f が右逆写像を持つとき、f を全射といい、f が左逆写像を持つとき、f を単射という。

既知の写像から別の新たな写像を構成する方法をいくつか示す。

写像の定義域をより小さな部分集合に取り換えることで写像の制限 (restriction) または縮小^[11]が定義される。すなわち、写像 f: X → Y と部分集合 S ⊆ X が任意に与えられたとき、任意の s ∈ S に対して f|_S(s) := f(s) と置くことにより定義される写像 f|_S: S → Y を写像 f の S への（定義域の）制限と呼ぶ。写像 h の適当な制限が f に一致するとき、h は f の延長 (continuation) または拡大^[12]もしくは拡張 (extension) であるという。終域の制限や延長を考えることもある。また写像の制限の記号は誤解のおそれが無い限り省略されることも多い。

ふたつの写像 f: X → Y, g: W → Y で、それらの定義域が交わりを持たない (X ∩ W = ∅) とき、これらのグラフの合併として写像の直和 f ⊕ g: X ∪ W → Y を定義する。これは具体的に

${\displaystyle (f\oplus g)(\xi )={\begin{cases}f(\xi )&(\xi \in X)\\g(\xi )&(\xi \in W)\end{cases}}}$

と書ける区分的に定義された写像である。より一般に、X ∩ W ≠ ∅ のとき、二つの写像の X ∩ W への制限が f|_X∩W = g|_X∩W を満たすとき、直和写像 f ⊕ g は well-defined で、

${\displaystyle (f\oplus g)(\xi )={\begin{cases}f(\xi )&(\xi \in X\smallsetminus W)\\f|_{X\cap W}(\xi )=g|_{X\cap W}(\xi )&(\xi \in X\cap W)\\g(\xi )&(\xi \in W\smallsetminus X)\end{cases}}}$

を満たす。直和 f ⊕ g は f, g の共通の延長として最小であり、直和のグラフはそれぞれの写像のグラフの合併である。直和は可換である。

さらに一般の場合に、f: X → Y の g: W → Y による上書き和 (override union) と呼ばれる g の延長 f ⊕ g: X ∪ W → Y が g および f|_X∖W のグラフの合併として与えられ、

${\displaystyle (f\oplus g)(\xi )={\begin{cases}f(\xi )&(\xi \in X)\\g(\xi )&(\xi \in W\smallsetminus X)\end{cases}}}$

と書ける。上書き和は一般には可換でない。

ふたつの写像 f: X → Z, g: Y → W に対して、写像の直積 f × g: X × Y → Z × W は

${\displaystyle (f\times g)(x,y):=(f(x),g(y))\quad (x\in X,\,y\in Y)}$

で与えられる。

任意の写像 f: X → Y に対し、X 上の二項関係 ∼_f を

${\displaystyle a\sim _{f}b\iff f(a)=f(b)}$

で定めると ∼_f は同値関係で、写像 f に付随する同値関係^[13]と呼ばれる。この同値関係による類別を考えることにより X は等位集合 C(y) = f⁻¹(y) (y ∈ Y) の和に分割される。このとき、商集合 X/∼_f からの写像

${\displaystyle \varphi \colon X/{\sim _{f}}\to \operatorname {ran} (f)(\subset Y);\;C(y)\mapsto y}$

は well-defined で、f の同値関係 ∼_f による商写像あるいは f に付随する全単射^[14]と呼ぶ。写像系列

${\displaystyle f\colon X{\stackrel {\pi }{{}\twoheadrightarrow {}}}X/{\sim _{f}}{\stackrel {\varphi }{{}\to {}}}\operatorname {ran} (f){\stackrel {\iota }{{}\hookrightarrow {}}}Y,}$

あるいは等式 f = ι ∘ φ ∘ π （ただし、π は自然な全射、ι は自然な単射）を写像 f の標準分解^[14]と呼ぶ。

X から Y への写像全体の成す集合は配置集合^[15] (独: Belegungsmenge^[16]) と呼ばれ、しばしば指数記法に従って Y^X（あるいは ^XY）と書かれる。圏論の言葉で言えば配置集合は集合と写像の圏の指数である^[要出典]。配置集合は ${\displaystyle [X\to Y],\ {\mathcal {F}}(X,Y),\ \operatorname {Map} (X,Y)}$ とも書かれる。

• 濃度の冪は配置集合の濃度と定義される: |B^A| = |B|^|A|[17]。

カリー化 ^A×BC → ^A(^BC) は^[要出典]

${\displaystyle f\mapsto g\quad (C\ni f(a,b)=g(a)(b);\;g:A\to [B\to C])}$^[要出典]

のように二変数写像をある種一変数化する、配置集合の間の同型である^[要出典]。

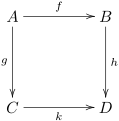
複数の集合と写像を一度に扱う必要があるとき、図式や系列と呼ばれる道具を用いると記述が簡素になる。ホモロジー代数や圏論の文脈ではよく用いられる。写像の図式^[18]とは、いくつかの集合を頂点とし、それらの集合間の写像を有向辺にもつようなグラフである。簡単な図式の例としては鎖 ${\displaystyle A_{1}{\stackrel {f_{1}}{{}\to {}}}A_{2}{\stackrel {f_{2}}{{}\to {}}}A_{3}}$ や

• 
  写像の合成: 可換三角形
• 
  可換矩形

などを挙げることができる。任意の頂点から別の任意の頂点への写像が経路の取り方に依らないとき、図式は可換であるという^[19]。例えば h = g ∘ f のとき図式

は可換であり、逆もまた成り立つ。

一般には、定義域と始域が異なる（値の定められていない始域の元が存在する）という場合も考え得る。集合 A, B の元の順序対からなる集合（すなわち二項関係）G_f が

• 右一意性: (x, y₁) ∈ G_f かつ (x, y₂) ∈ G_f ならば y₁ = y₂

をみたすとき G_f は A から B への関数関係であると言われる。このとき、三つ組 f := (A, B, G_f) をこの関数関係 G_f から定まる A から B への部分写像と呼び^{[注釈 4]}、f: A → B で表す。部分写像 f: A → B すなわち G_f ⊆ A × B の定義域 dom(f) と値域 ran(f) は次のように定義される：

${\displaystyle \operatorname {dom} (f)=\{x\mid \exists y((x,y)\in G_{f})\}\subseteq A,\quad \operatorname {ran} (f)=\{y\mid \exists x((x,y)\in G_{f})\}\subseteq B.}$

写像の定義の際には課した関係の全域性は、部分写像 f の定義域 dom(f) が始域 A に一致することをいうものであり、全域的な部分写像を特に全域写像 (total mapping) と呼ぶ。すなわち、全域写像は写像の同義語である^{[注釈 5]}。

写像の多変数化による一般化を考えると、それは始域を何らかの直積集合に取り換えた通常の意味の写像として扱える。とくに一つの集合 M に対して M × M ×…× M → M なる形の多変数写像は M の複数の元から別の新しい元を作り出す操作と見做して算法と呼ばれる^[20]。

多値の関数の場合も終域を直積集合に取り換えた写像として定式化することができる場合もあり、例えばベクトル値関数 はスカラー値関数の直積として理解できる。しかし単純にそのように捉えることができない場合、あるいは捉えないほうがよい場合もある。例えば多価の複素解析関数は、分岐切断を超えてそれぞれの分枝の間に素性の良い関係性を記述することができ、適当なリーマン面上で定義された通常の関数と考えることが有効である。

写像は集合と写像の圏における射であり、一般に具体圏（英語版）における射はある種の写像として与えられるが、一般の圏における射は必ずしも写像でない。

圏の間の関手は、集合の間の写像と似た概念だが、対象同士の対応関係とともに対象間の射についても同時に対応関係を記述する。さらに、関手間の射として自然変換の概念が定式化される。

• ニコラ・ブルバキ 著、前原昭二 訳『集合論 要約』〈数学原論〉1968年。 
• Halmos, Paul R. (1970). Naive Set Theory. Springer-Verlag. ISBN 0-387-90092-6. https://books.google.co.jp/books?id=x6cZBQ9qtgoC&redir_esc=y&hl=ja 
• ジョン L. ケリ－ 著、児玉之宏 訳『位相空間論』吉岡書店、1968年。 
• Kunen, Kenneth (1980). Set Theory An Introduction to Independence Proofs. North-Holland. ISBN 0-444-86839-9 
• Lang, Serge (1971), Linear Algebra (2nd ed.), Addison-Wesley 
• 松本, 幸夫『多様体の基礎』東京大学出版会〈基礎数学5〉、1988年。ISBN 978-4-13-062103-8。 
• 松坂和夫『集合・位相入門』岩波書店、1968年。ISBN 4-00-005424-4。 

• 射 (圏論)
• 列 (数学)
• 族 (数学)

• Weisstein, Eric W. "Map". mathworld.wolfram.com (英語).
• mapping - PlanetMath.（英語）
• 松本眞 (2004年). “代数系入門” (PDF). 広島大学 理学部数学科 松本研究室. 2012年5月閲覧。
• 『写像』 - コトバンク