|
Gruppo fondamentaleIn topologia, il gruppo fondamentale permette di analizzare la forma di un oggetto e tradurlo in forma algebrica. L'oggetto da analizzare deve essere uno spazio topologico (ad esempio un sottoinsieme del piano, dello spazio, o di un qualsiasi spazio euclideo). Il risultato della traduzione è un gruppo, detto appunto il gruppo fondamentale dello spazio. Definizione intuitiva Prendiamo come esempio il toro: il gruppo fondamentale del toro è un oggetto algebrico che ne cattura la forma, e che quindi codifichi la presenza di un "buco". Come sempre in topologia, questo oggetto deve dipendere solo dalla forma del toro e non dalla sua particolare posizione e rappresentazione nello spazio. Il gruppo fondamentale è definito usando le curve sul toro (dette lacci) che partono da un punto p e tornano a p. Ad esempio, la curva mostrata a destra. Questo laccio non cattura però informazioni importanti sulla forma del toro, perché può essere deformato in modo continuo (tramite una omotopia) senza uscire dalla superficie torica, fino a diventare arbitrariamente piccolo.  I due lacci a e b mostrati nella figura a sinistra, invece, sono molto più rappresentativi: proprio a causa del buco centrale, nessuno dei due può essere deformato ad un laccio piccolo senza uscire dalla superficie torica. E inoltre non è possibile ottenere b deformando a. Queste sono proprietà intrinseche del toro: tramite queste considerazioni ci si accorge dell'esistenza di un buco "dall'interno", senza usare lo spazio tridimensionale che lo contiene. 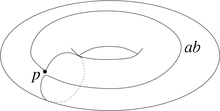 I due lacci a e b possono essere composti in modo da ottenere un terzo laccio, che prima fa un giro come a e poi ne fa un altro come b. Il nuovo laccio può essere chiamato ab. In questo modo, dando dei nomi ai lacci, considerandoli a meno di deformazioni, e componendoli si ottiene un oggetto basilare dell'algebra: un gruppo. Ad esempio in questo caso si ottiene il gruppo abeliano Z x Z dato da tutte le coppie (x, y) di interi, generato dai lacci a e b che si traducono rispettivamente in (1, 0) e (0, 1). Definizione formaleLacci (o cappi)Sia uno spazio topologico connesso per archi e un suo punto fissato. Come accennato sopra, un laccio (o cappio) centrato in è una funzione continua tale che . In altre parole, è un circuito o cammino chiuso, cioè un arco che parte e torna in .  Due lacci e , entrambi centrati in , possono essere concatenati: il laccio gira prima lungo e quindi lungo , ciascuno a velocità doppia. In altre parole: Scopo di questa costruzione è ottenere un gruppo, i cui elementi sono i lacci e la cui operazione è data dal concatenamento. Con queste definizioni però nessuno degli assiomi necessari è soddisfatto! Ad esempio, non è valida neppure la proprietà associativa: infatti i lacci fanno gli stessi percorsi ma con velocità differenti e sono quindi lacci distinti: la prima gira lungo in un tempo 1/4, mentre la seconda gira lungo in un tempo 1/2. Possono però essere considerati lo stesso laccio a meno di omotopia. Omotopia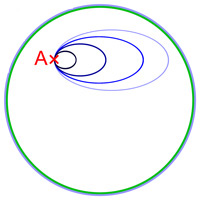  La definizione di laccio appare troppo "rigida": per ovviare a questo problema si considerano i lacci a meno di deformazioni, cioè di omotopie. Una omotopia fra due lacci e è una funzione continua che trasforma in tramite lacci centrati in . In altre parole, valgono le relazioni e inoltre Due lacci sono equivalenti se esiste una omotopia che li collega. In questo modo si ottiene una relazione d'equivalenza, e quindi un insieme quoziente (dato appunto dalle classi di equivalenza) che viene normalmente indicato con La classe di equivalenza di un laccio è indicata con , ed è quindi un elemento di . Questo insieme, dotato dell'operazione di concatenamento, risulta effettivamente essere un gruppo, chiamato gruppo fondamentale.  Più dettagliatamente, valgono i fatti seguenti:
Il gruppo fondamentale di uno spazio topologico non è necessariamente abeliano. EsempiSpazi semplicemente connessiUno spazio topologico con gruppo fondamentale banale (cioè avente un solo elemento) si dice semplicemente connesso. Gli spazi topologici semplicemente connessi hanno un ruolo fondamentale in geometria. La palla -dimensionale (e quindi in particolare l'intervallo) è semplicemente connessa. In generale ogni spazio contraibile, cioè omotopicamente equivalente ad un punto, è semplicemente connesso. Quindi un qualsiasi insieme convesso dello spazio euclideo è semplicemente connesso. Anche la retta e il piano sono semplicemente connessi.  La sfera -dimensionale con n maggiore o uguale a due è semplicemente connessa, benché non sia contraibile. CirconferenzaLo spazio topologico più semplice non semplicemente connesso è la circonferenza, indicata con il simbolo . Il suo gruppo fondamentale è isomorfo al gruppo additivo dei numeri interi : il numero intero associato ad un laccio di è il numero di volte che questo "gira" intorno ad essa. Il seguente esempio illustra un'applicazione del gruppo fondamentale: pensiamo di partire per un viaggio da un punto della terra e fare un certo percorso intorno ad essa fino a ritornare al punto di partenza. Supponiamo di viaggiare abbastanza più lentamente del sole e di non andare oltre i circoli polari. In questo viaggio supponiamo di vedere il sole sorgere e tramontare 57 volte, mentre sappiamo dal nostro orologio che sono passati 51 giorni soltanto. Da dove arrivano questi 6 giorni in più? Ebbene, la terra senza le calotte polari ha lo stesso gruppo fondamentale di e il nostro percorso, secondo l'isomorfismo con i numeri interi citato sopra, è associato al numero -6; con qualunque altro percorso omotopo (sempre togliendo le calotte polari) avremmo ottenuto lo stesso risultato. Questo perché a ogni giro intorno alla terra corrisponde un'alba e un tramonto in più o in meno; dunque per contare i giri intorno alla terra basta fare la differenza tra questi e i giorni effettivi. ProprietàDipendenza dal punto baseIl gruppo fondamentale di uno spazio topologico connesso per archi non dipende dal punto base scelto. Per questo motivo il punto base spesso viene omesso, e si parla di gruppo fondamentale dello spazio , indicato con Più precisamente, se è un altro punto, esiste un isomorfismo La funzione è costruita a partire da un arco che collega e . L'isomorfismo dipende dalla scelta dell'arco e quindi non è canonico: per questo motivo in alcuni contesti la scelta del punto base è comunque essenziale. Proprietà funtorialiOgni funzione continua fra spazi topologici tale che induce un omomorfismo tra i corrispettivi gruppi fondamentali. Il gruppo fondamentale trasforma quindi oggetti e mappe topologiche in oggetti e mappe algebriche. Usando il linguaggio della teoria delle categorie, si dice che è un funtore covariante dalla categoria degli spazi topologici puntati (cioè con punto base) in quella dei gruppi. In particolare, se è un omeomorfismo la funzione indotta a livello di gruppi è un isomorfismo di gruppi. Quindi spazi topologici omeomorfi hanno gruppi fondamentali isomorfi. Equivalenza omotopicaDue spazi topologici omotopicamente equivalenti hanno gruppi fondamentali isomorfi. Questo vuol dire che il gruppo fondamentale è una quantità che non distingue (non "vede") l'omotopia. In generale, due funzioni tali che omotope (tramite una omotopia relativa a , cioè in cui ogni livello della deformazione manda in ) inducono gli stessi omomorfismi Spazi prodottoIl gruppo fondamentale del prodotto di due spazi topologici e è il prodotto diretto dei gruppi dei due spazi. In altre parole: Poiché il toro è omeomorfo al prodotto di due circonferenze il suo gruppo fondamentale è . ApplicazioniIntegrazione di funzioni olomorfeLo studio del gruppo fondamentale ha applicazioni in analisi complessa; in particolare, data una funzione olomorfa l'integrale di lungo una curva si conserva per omotopia, ed è possibile vedere questo integrale come un omomorfismo di gruppi Se è una funzione meromorfa su un dominio semplicemente connesso, l'immagine di è generata dai residui della nei suoi poli moltiplicati per . StrumentiTeorema di Van Kampen Il teorema di Van Kampen permette di calcolare il gruppo fondamentale di uno spazio topologico a partire dai gruppi fondamentali di alcuni suoi "pezzi". Più precisamente, se è ricoperto da due aperti con e tutti connessi per archi, il gruppo fondamentale di è il prodotto amalgamato dei gruppi di e , amalgamati sul gruppo fondamentale dell'intersezione. In particolare, se e sono semplicemente connessi, allora lo è anche . In questo modo si dimostra ad esempio che le sfere di dimensione sono tutte semplicemente connesse.  RivestimentiLa nozione topologica di rivestimento è strettamente collegata a quella di gruppo fondamentale. Un rivestimento è una funzione fra spazi topologici (connessi per archi) simile ad un omeomorfismo, ma non necessariamente iniettiva. La correlazione con il gruppo fondamentale sta nel fatto che i rivestimenti di corrispondono essenzialmente ai sottogruppi di . Il rivestimento corrispondente al sottogruppo banale è detto rivestimento universale ed è un oggetto molto importante in topologia. GeneralizzazioniGruppi di omotopiaLa costruzione del gruppo fondamentale di uno spazio topologico può essere variata sostituendo i lacci con sfere di dimensione arbitraria. L'oggetto che ne risulta è sempre un gruppo, detto gruppo di omotopia e indicato con Con si ottiene il gruppo fondamentale. Gruppo dei cammini marginali di un complesso simplicialeSe X è un complesso simpliciale connesso, un cammino marginale in X si definisce come una catena di vertici connessi mediante i margini in X. Due cammini marginali si dicono "equivalenti al margine" se uno può essere ottenuto dall'altro spostandosi successivamente tra un margine e i due margini opposti di un triangolo in X. Se v è un vertice fisso in X, un laccio marginale presso v è un cammino marginale che parte e finisce presso v. Il gruppo dei cammini marginali E(X, v) si definisce come l'insieme di classi di equivalenza marginale dei lacci marginali presso v, con il prodotto e l'inverso definiti dalla concatenazione e dall'inversione dei lacci marginali. Il gruppo dei cammini marginali è naturalmente isomorfo, per π1(|X|, v), al gruppo fondamentale della realizzazione geometrica |X| di X. Poiché dipende soltanto dai 2-scheletri X2 di X (cioè i vertici, i margini e i triangoli di X), i gruppi π1(|X|,v) e π1(|X2|, v) sono isomorfici. Il gruppo dei cammini marginali può essere descritto esplicitamente in termini di generatori e relazioni. Se T è un albero ricoprente massimo nell'1-scheletro di X, allora E(X, v) è canonicamente isomorfico rispetto al gruppo con i generatori (i cammini marginali orientati di X che non compaiono in T) e con relazioni (le equivalenze marginali che corrispondono ai triangoli in X). Un risultato simile è valido se T è sostituito da un qualsiasi sottocomplesso semplicemente connesso di X – in particolare contraibile –. Questo dà spesso un modo pratico di calcolare i gruppi fondamentali e può essere usato per mostrare che ogni gruppo finitamente presentato sorge come il gruppo fondamentale di un complesso simpliciale finito. È anche uno dei metodi classici usati per le superfici topologiche, che sono classificate in base ai loro gruppi fondamentali. Lo spazio universale di rivestimento di un complesso simpliciale connesso finito X può essere descritto direttamente come un complesso simpliciale usando i cammini marginali. I suoi vertici sono coppie (w,γ) dove w è un vertice di X e γ una classe di equivalenza marginale di cammini da v a w. I k-simplessi contenenti (w,γ) corrispondono naturalmente ai k-simplessi contenenti w. Ciascun nuovo vertice u del k-simplesso dà un margine wu e quindi, per concatenazione, un nuovo cammino γu da v a u. i punti (w,γ) e (u, γu) sono i vertici del simplesso "trasportato" nello spazio universale di rivestimento. Il gruppo dei cammini marginali agisce naturalmente per concatenazione, preservando la struttura simpliciale, e lo spazio quoziente è appunto X. È risaputo che questo metodo può essere usato anche per calcolare il gruppo fondamentale di uno spazio topologico arbitrario. Ciò era senza dubbio noto a Čech e Leray e apparve esplicitamente come un'osservazione in un saggio di Weil (1960); vari altri autori come L. Calabi, W-T. Wu e N. Berikashvili hanno anch'essi pubblicato prove. Nel caso più semplice di uno spazio compatto X con rivestimento aperto finito nel quale tutte le intersezioni finite non vuote degli insiemi aperti nel rivestimento sono contraibili, Il gruppo fondamentale può essere identificato con il gruppo dei cammini marginali del complesso simpliciale corrispondente al nerbo del rivestimento. Bibliografia
Voci correlateAltri progetti
Collegamenti esterni
|


![{\displaystyle \gamma :[0,1]\to X}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd7494ff58ac924ec9cc7240baef18445f317c14)



![{\displaystyle \gamma *\lambda :[0,1]\to X\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/646732a071b751aaa385fa73ab1839a04f40077f)
![{\displaystyle \gamma *\lambda (t)=\left\{{\begin{matrix}\gamma (2t),&{\mbox{se }}t\in [0,1/2]\\\lambda (2t-1),&{\mbox{se }}t\in [1/2,1]\end{matrix}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e84e5770ae3e92c6792c84b5067e50ee4b9e8afb)



![{\displaystyle F:[0,1]\times [0,1]\to X}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8935dc7cebf2aa3d676da7e02082cfd94ea5f10e)



![{\displaystyle [\gamma ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7b30910bca19778c71191d14f63ef6517dd9c04a)
![{\displaystyle [\gamma *\lambda ]=[\gamma ]*[\lambda ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/71667e162c0c6f7eb9bdb793aa397d04d4467f13)








































