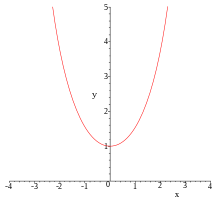
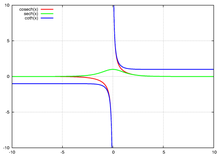
Wykres funkcji sinhWykres funkcji cosh to krzywa łańcuchowa . Wykresy funkcji sinus, cosinus i tangens hiperboliczny Wykresy funkcji cotangens, secans i cosecans hiperboliczny Funkcje hiperboliczne – zbiór sześciu funkcji zdefiniowanych przez działania arytmetyczne na funkcji wykładniczej [1]
nazwa
symbole
wzory
sinus hiperboliczny
sinh
x
,
sh
x
{\displaystyle \sinh x,\operatorname {sh} x}
e
x
−
e
−
x
2
{\displaystyle {\frac {e^{x}-e^{-x}}{2}}}
cosinus hiperboliczny
cosh
x
,
ch
x
{\displaystyle \cosh x,\operatorname {ch} x}
e
x
+
e
−
x
2
{\displaystyle {\frac {e^{x}+e^{-x}}{2}}}
tangens hiperboliczny
tgh
x
,
th
x
{\displaystyle \operatorname {tgh} x,\operatorname {th} x}
sinh
x
cosh
x
=
e
x
−
e
−
x
e
x
+
e
−
x
{\displaystyle {\frac {\sinh x}{\cosh x}}={\frac {e^{x}-e^{-x}}{e^{x}+e^{-x}}}}
cotangens hiperboliczny
ctgh
x
,
cth
x
{\displaystyle \operatorname {ctgh} x,\operatorname {cth} x}
cosh
x
sinh
x
=
e
x
+
e
−
x
e
x
−
e
−
x
{\displaystyle {\frac {\cosh x}{\sinh x}}={\frac {e^{x}+e^{-x}}{e^{x}-e^{-x}}}}
secans hiperboliczny
sech
x
{\displaystyle \operatorname {sech} x}
1
cosh
x
=
2
e
x
+
e
−
x
{\displaystyle {\frac {1}{\cosh x}}={\frac {2}{e^{x}+e^{-x}}}}
cosecans hiperboliczny
cosech
x
{\displaystyle \operatorname {cosech} x}
1
sinh
x
=
2
e
x
−
e
−
x
{\displaystyle {\frac {1}{\sinh x}}={\frac {2}{e^{x}-e^{-x}}}}
Funkcje te mogą mieć dziedzinę rzeczywistą lub zespoloną i zalicza się je do funkcji elementarnych [1] funkcji trygonometrycznych . Nazwę swoją zawdzięczają temu, że para liczb (cosh(t),sinh(t)) tworzy wykres hiperboli
x
2
−
y
2
=
1
{\displaystyle x^{2}-y^{2}=1}
Przez funkcje hiperboliczne można definiować funkcje polowe , inaczej funkcje area lub areafunkcje – są to funkcje odwrotne tych hiperbolicznych, wyrażane też przez logarytmy .
Dzieje
Do nauki wprowadził je włoski matematyk Vincenzo Riccati , który publikował swoje rozważania w Opusculorum ad res physicas et mathematicas pertinentium , wydawanym między 1757 a 1762 rokiem[2] sinus i cosinus hiperbolico i zastosował skróty Sh i Ch, stosowane do dziś w Rosji i we Francji .
Szwajcarski matematyk Johann Heinrich Lambert upowszechnił te funkcje, pokazując ich zastosowanie w trygonometrii w dziele Mémoire sur quelques propriétés remarquables des quantités transcendentes circulaires et logarithmiques (1762). Lambert zostawił im nazwy zaproponowane przez Riccatiego, ale nadał im skróty sinh i cosh stosowane do dnia dzisiejszego[3]
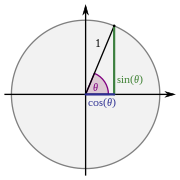
Zbiór punktów płaszczyzny o współrzędnych postaci
(
cos
x
,
sin
x
)
{\displaystyle (\cos x,\sin x)}
okręgiem (jednostkowym ), analogicznie zbiór punktów o współrzędnych postaci
(
cosh
x
,
sinh
x
)
{\displaystyle (\cosh x,\sinh x)}
hiperbolę .
Prawdziwe są również wzory:
sinh
2
t
=
2
sinh
t
cosh
t
,
{\displaystyle \sinh 2t=2\sinh t\cosh t,}
cosh
2
t
=
cosh
2
t
+
sinh
2
t
,
{\displaystyle \cosh 2t=\cosh ^{2}t+\sinh ^{2}t,}
sinh
x
+
cosh
x
=
e
x
.
{\displaystyle \sinh x+\cosh x=e^{x}.}
Ponadto korzystając ze wzoru Eulera
e
i
x
=
cos
x
+
i
sin
x
,
{\displaystyle e^{ix}=\cos x+i\sin x,}
można przedstawić związek funkcji hiperbolicznych z trygonometrycznymi, wyrażony w liczbach zespolonych :
sinh
i
x
=
i
sin
x
,
{\displaystyle \sinh ix=i\sin x,}
cosh
i
x
=
cos
x
,
{\displaystyle \cosh ix=\cos x,}
tgh
i
x
=
i
tg
x
,
{\displaystyle \operatorname {tgh} ix=i\operatorname {tg} x,}
ctgh
i
x
=
−
i
ctg
x
,
{\displaystyle \operatorname {ctgh} ix=-i\operatorname {ctg} x,}
skąd:
sinh
x
=
−
i
sin
i
x
,
{\displaystyle \sinh x=-i\sin ix,}
cosh
x
=
cos
i
x
,
{\displaystyle \cosh x=\cos ix,}
tgh
x
=
−
i
tg
i
x
,
{\displaystyle \operatorname {tgh} x=-i\operatorname {tg} ix,}
ctgh
x
=
i
ctg
i
x
.
{\displaystyle \operatorname {ctgh} x=i\operatorname {ctg} ix.}
Ponieważ funkcje trygonometryczne są okresowe wzdłuż osi liczb rzeczywistych , to funkcje hiperboliczne są okresowe wzdłuż osi liczb urojonych z okresem
2
π
i
{\displaystyle 2\pi i}
π
i
{\displaystyle \pi i}
Jeśli
φ
{\displaystyle \varphi }
złotą proporcję , to:
sinh
ln
φ
=
1
2
,
{\displaystyle \sinh \ln \varphi ={\tfrac {1}{2}},}
cosh
ln
φ
=
1
2
5
.
{\displaystyle \cosh \ln \varphi ={\tfrac {1}{2}}{\sqrt {5}}.}
Odpowiednikiem „jedynki trygonometrycznej ”
sin
2
x
+
cos
2
x
=
1
{\displaystyle \sin ^{2}x+\cos ^{2}x=1}
jest tzw. „jedynka hiperboliczna ”:
cosh
2
x
−
sinh
2
x
=
1.
{\displaystyle \cosh ^{2}x-\sinh ^{2}x=1.}
Z każdej tożsamości trygonometrycznej można otrzymać tożsamość hiperboliczną przez użycie związku pomiędzy funkcjami trygonometrycznymi i hiperbolicznymi.
sinh
′
x
=
cosh
x
,
{\displaystyle \sinh 'x=\cosh x,}
cosh
′
x
=
sinh
x
,
{\displaystyle \cosh 'x=\sinh x,}
tgh
′
x
=
1
cosh
2
x
=
1
−
tgh
2
x
,
{\displaystyle \operatorname {tgh} 'x={\frac {1}{\cosh ^{2}x}}=1-\operatorname {tgh} ^{2}x,}
ctgh
′
x
=
−
1
sinh
2
x
=
1
−
ctgh
2
x
.
{\displaystyle \operatorname {ctgh} 'x={\frac {-1}{\sinh ^{2}x}}=1-\operatorname {ctgh} ^{2}x.}
Szeregi potęgowe
sinh
z
=
∑
n
=
0
∞
z
2
n
+
1
(
2
n
+
1
)
!
=
z
+
z
3
3
!
+
z
5
5
!
+
z
7
7
!
+
…
,
{\displaystyle \sinh z=\sum _{n=0}^{\infty }{\frac {z^{2n+1}}{(2n+1)!}}=z+{\frac {z^{3}}{3!}}+{\frac {z^{5}}{5!}}+{\frac {z^{7}}{7!}}+\dots ,}
cosh
z
=
∑
n
=
0
∞
z
2
n
(
2
n
)
!
=
1
+
z
2
2
!
+
z
4
4
!
+
z
6
6
!
+
…
{\displaystyle \cosh z=\sum _{n=0}^{\infty }{\frac {z^{2n}}{(2n)!}}=1+{\frac {z^{2}}{2!}}+{\frac {z^{4}}{4!}}+{\frac {z^{6}}{6!}}+\dots }
Iloczyny nieskończone
sinh
x
=
x
∏
n
=
1
∞
(
1
+
x
2
π
2
n
2
)
,
{\displaystyle \sinh x=x\prod _{n=1}^{\infty }\left(1+{\frac {x^{2}}{\pi ^{2}n^{2}}}\right),}
cosh
x
=
∏
n
=
1
∞
(
1
+
x
2
π
2
(
n
−
1
2
)
2
)
.
{\displaystyle \cosh x=\prod _{n=1}^{\infty }\left(1+{\frac {x^{2}}{\pi ^{2}(n-{\frac {1}{2}})^{2}}}\right).}
Przypisy
↑ a b funkcje hiperboliczne Encyklopedia PWN Wydawnictwo Naukowe PWN [dostęp 2021-10-02] .↑ Robert E. Bradley, Lawrence A. D’Antonio, Charles Edward Sandifer, Euler at 300: an appreciation , Mathematical Association of America, 2007, s. 100.
↑ Georg F. Becker, Hyperbolic functions , Read Books, 1931, s. xlviii.